Câu hỏi:
15/02/2025 156
Cho \(\Delta ABC\) có các đường trung tuyến \(BD,CE\). Gọi \(M,N\) theo thứ tự là trung điểm của \(BE,CD\). Gọi \(I,K\) theo thứ tự là giao điểm của \(MN\) với \(BD\) và \(CE\). Chứng minh rằng:
a) \(DE\parallel BC\).
b) \(MN\parallel BC.\)
c) \(MI = IK = KN.\)
Cho \(\Delta ABC\) có các đường trung tuyến \(BD,CE\). Gọi \(M,N\) theo thứ tự là trung điểm của \(BE,CD\). Gọi \(I,K\) theo thứ tự là giao điểm của \(MN\) với \(BD\) và \(CE\). Chứng minh rằng:
a) \(DE\parallel BC\).
b) \(MN\parallel BC.\)
c) \(MI = IK = KN.\)
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
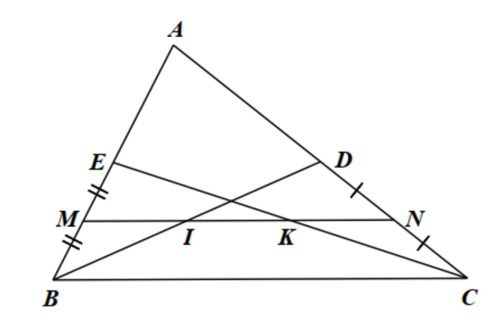
a) Trong \(\Delta ABC\) có các đường trung tuyến \(BD,CE\) nên \(D\) là trung điểm của \(AC\), \(E\) là trung điểm của \(AB\) nên \(ED\) là đường trung bình của \(\Delta ABC\).
Suy ra \(ED = \frac{1}{2}BD\) và \(ED\parallel BC\) (tính chất đường trung bình của tam giác)
b) Ta có: \(E\) là trung điểm của \(AB\) nên \(AE = EB = \frac{1}{2}AB.\)
Mà \(M\) là trung điểm của \(EB\) nên \(EM = MB = \frac{1}{2}EB = \frac{1}{4}AB\) hay \(\frac{{MB}}{{AB}} = \frac{1}{4}\).
Lại có \(N\) là trung điểm của \(CD\) nên \(NC = DN = \frac{1}{2}DC = \frac{1}{4}AC\) hay \(\frac{{NC}}{{AC}} = \frac{1}{4}\).
Suy ra \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}} = \frac{1}{4}\).
Xét \(\Delta ABC\) có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) nên \(MN\parallel BC\) (định lí Thalès đảo).
c) Ta có \(MN\parallel BC\) (câu b) và \(ED\parallel BC\) (câu a) nên \(ED\parallel MN\parallel BC\).
Xét \(\Delta BDE\) có \(M\) là trung điểm của \(EB\) và \(MI\parallel ED\) (do \(ED\parallel MN\parallel BC\)).
Suy ra \(I\) là trung điểm của \(BD\) hay \(IB = ID\).
Khi đó \(MI\) là đường trung bình của \(\Delta BDE\) nên \(MI = \frac{1}{2}ED\).
Xét \(\Delta CDE\) ta cũng có \(N\) là trung điểm của \(CD\) và \(NK\parallel ED\) (do \(ED\parallel MN\parallel BC\))
Suy ra \(K\) là trung điểm của \(EC\) hay \(EK = KC\).
Khi đó, \(KN\) là đường trung bình của \(\Delta CDE\) nên \(NK = \frac{1}{2}ED\), trong \(\Delta CBE\) có \(MK = \frac{1}{2}BC\).
Ta có: \(IK = MK - MI = \frac{1}{2}BC - \frac{1}{2}ED = ED - \frac{1}{2}DE = \frac{1}{2}DE\).
Do đó, \(MI = IK = KN.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Trong các mặt hàng trên, sản phẩm được giảm giá nhiều nhất là áo sơ mi giảm \(35\% \), sản phẩm được giảm giá ít nhất là quần Jeans giảm \(10\% \).
Ta có biểu đồ biểu diễn các mặt hàng giảm giá là
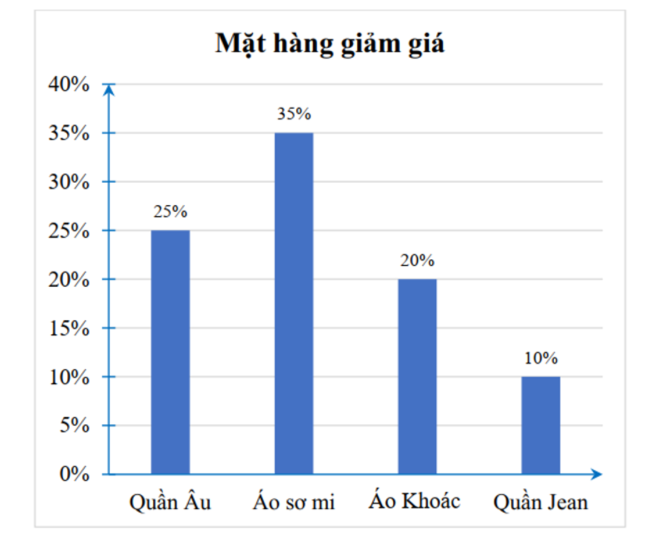
b) Theo đề, áo sơ mi giảm giá \(35\% \), giá sau giảm là \(325{\rm{ 000}}\) đồng. do đó, mỗi chiếc áo sơ mi nguyên giá sẽ là \(325{\rm{ 000:}}\left( {100\% - 25\% } \right) = 500{\rm{ }}000\) đồng.
Giá một chiếc quần Âu sau khi giảm là \(\frac{{1{\rm{ }}850{\rm{ }}000 - 325{\rm{ }}000}}{4} = 300{\rm{ }}000\) (đồng)
Giá của chiếc quần Âu trước khi giảm là: \(300{\rm{ }}000:\left( {100\% - 25\% } \right) = 400{\rm{ }}000\) đồng.
Lời giải
Đáp án đúng là: B
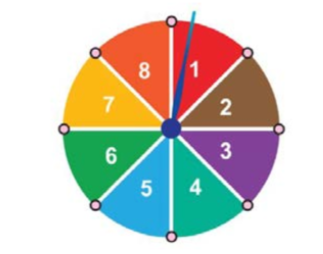
Các kết quả có thể xảy ra khi quay đĩa một lần là \(8\).
Do đó, nếu \(k\) là số kết quả thuận lợi cho biến cố thì xác suất của biến cố đó là \(\frac{k}{8}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận