Cho ba đường thẳng \(\left( {{d_1}} \right):y = - 2x\), \(\left( {{d_2}} \right):y = 1,5x + 7\), \(\left( {{d_3}} \right):y = mx + 4\). Tìm giá trị của tham số \(m\) để ba đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right),\left( {{d_3}} \right)\) đồng quy.

a) Xét phương trình hoành độ giao điểm: \(2x = - x + 3\) suy ra \(2x + x = 3\) hay \(3x = 3\).

Do đó, \(x = 1.\)

Thay \(x = 1\) vào \(\left( d \right):y = 2x\) ta được \(y = 2\).

Vậy giao điểm của hai đường thẳng \(\left( d \right)\) và \(\left( {d'} \right)\) là \(A\left( {1;2} \right)\).

b) Thay \(y = 0\) vào \(\left( {d'} \right)\), ta được: \( - x + 3 = 0\) hay \(x = 3\).

Vậy giao điểm của \(\left( {d'} \right)\) với trục \(Ox\) là \(B\left( {3;0} \right)\).

Ta có đồ thị sau:

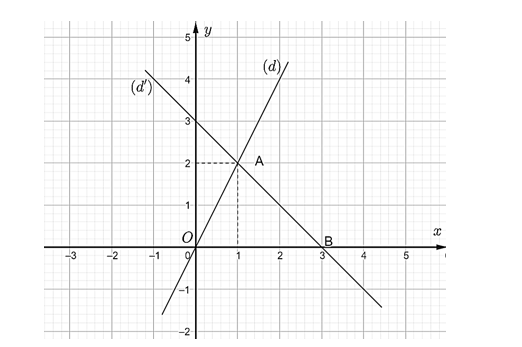
Từ đồ thị, ta có \(OB = 3\).

Chiều cao từ \(A\) xuống \(OB\) chính là \(2\).

Vậy diện tích của tam giác \(AOB\) là \(\frac{1}{2}.2.3 = 3\) (đvdt).

\(\frac{{x - 1}}{{2015}} + \frac{{x - 3}}{{2013}} = \frac{{x - 5}}{{2011}} + \frac{{x - 7}}{{2009}}\)

\(\frac{{x - 1}}{{2015}} - 1 + \frac{{x - 3}}{{2013}} - 1 = \frac{{x - 5}}{{2011}} - 1 + \frac{{x - 7}}{{2009}} - 1\)

\(\frac{{x - 2016}}{{2015}} + \frac{{x - 2016}}{{2013}} = \frac{{x - 2016}}{{2011}} + \frac{{x - 2016}}{{2009}}\)

\(\frac{{x - 2016}}{{2015}} + \frac{{x - 2016}}{{2013}} - \frac{{x - 2016}}{{2011}} - \frac{{x - 2016}}{{2009}} = 0\)

\(\left( {x - 2016} \right)\left( {\frac{1}{{2015}} + \frac{1}{{2013}} - \frac{1}{{2011}} - \frac{1}{{2009}}} \right) = 0\)

Nhận thấy \(\left( {\frac{1}{{2015}} + \frac{1}{{2013}} - \frac{1}{{2011}} - \frac{1}{{2009}}} \right) \ne 0\) nên \(x - 2016 = 0\) suy ra \(x = 2016\).

Vậy \(x = 2016\).