Câu hỏi:
15/02/2025 513
Cho ba đường thẳng \(\left( d \right):y = x + 2\); \(\left( {d'} \right):y = 3x + 2\) và \(\left( {d''} \right):y = \left( {4 - m} \right)x + 1 + m\). Tìm giá trị của tham số \(m\) để ba đường thẳng đồng quy.
Cho ba đường thẳng \(\left( d \right):y = x + 2\); \(\left( {d'} \right):y = 3x + 2\) và \(\left( {d''} \right):y = \left( {4 - m} \right)x + 1 + m\). Tìm giá trị của tham số \(m\) để ba đường thẳng đồng quy.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: \(1\)
• Xét phương trình hoành độ giao điểm của \(\left( d \right):y = x + 2\); \(\left( {d'} \right):y = 3x + 2\), ta có:
\(x + 2 = 3x + 2\) hay \(2x = 0\) suy ra \(x = 0.\)
Thay \(x = 0\) vào đường thẳng \(\left( d \right):y = x + 2\) được \(y = 2\).
Vậy giao điểm của hai đường thẳng \(\left( d \right),\left( {d'} \right)\) là \(A\left( {0;2} \right)\).
Để ba đường thẳng đồng quy thì \(\left( {d''} \right):y = \left( {4 - m} \right)x + 1 + m\) đi qua điểm \(A\left( {0;2} \right)\).
Thay \(x = 0,y = 2\) vào \(\left( {d''} \right)\) ta được: \(\left( {4 - m} \right).0 + 1 + m = 2\) suy ra \(m = 1.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: a) Đ b) S c) S d) S
Gọi \(x\) (giờ) là thời gian từ lúc xe con đi tới đuổi kịp xe khách (\(x > 0\)).
Thời gian xe khách đi tới lúc gặp xe con là \(x + 3\) (giờ).
Quãng đường đi được của xe con là \(50x\) (km).
Quãng đường đi được của xe khách là \(20\left( {x + 3} \right)\) (km).
Theo đề, ta có phương trình \(20\left( {x + 3} \right) = 50x\).
Giải phương trình, ta được:
\(20\left( {x + 3} \right) = 50x\)
\(20x + 60 = 50x\)
\(50x - 20x = 60\)
\(30x = 60\)
\(x = 2\) (thỏa mãn).
Vậy sau \(2\) giờ thì xe con đuổi kịp xe khách.
Lời giải
Đáp án đúng là: A
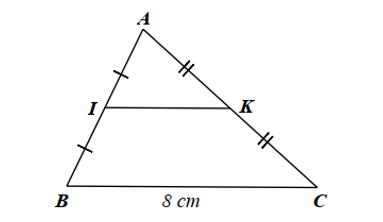
Xét \(\Delta ABC\) có \(I,K\) lần lượt là trung điểm của \(AB,AC\) nên \(IK\) là đường trung bình của tam giác.
Do đó, \(IK = \frac{1}{2}BC\) suy ra \(IK = 4{\rm{ cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận