Có 10 sinh viên chuẩn bị bước vào bài thi hỏi đáp, trong đó có 2 sinh viên giỏi (trả lời 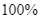 các câu hỏi), 3 sinh viên khá (trả lời
các câu hỏi), 3 sinh viên khá (trả lời 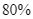 các câu hỏi), 5 sinh viên trung bình (trả lời
các câu hỏi), 5 sinh viên trung bình (trả lời 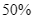 các câu hỏi). Giám khảo chọn ngẫu nhiên một sinh viên vào thi và ra đề gồm 4 câu hỏi (được lấy ngẫu nhiên từ 20 câu hỏi của đề cương ôn tập). Biết sinh viên này trả lời được cả 4 câu hỏi, tính xác suất để sinh viên đó là sinh viên khá.
các câu hỏi). Giám khảo chọn ngẫu nhiên một sinh viên vào thi và ra đề gồm 4 câu hỏi (được lấy ngẫu nhiên từ 20 câu hỏi của đề cương ôn tập). Biết sinh viên này trả lời được cả 4 câu hỏi, tính xác suất để sinh viên đó là sinh viên khá.
Có 10 sinh viên chuẩn bị bước vào bài thi hỏi đáp, trong đó có 2 sinh viên giỏi (trả lời ![]() các câu hỏi), 3 sinh viên khá (trả lời
các câu hỏi), 3 sinh viên khá (trả lời ![]() các câu hỏi), 5 sinh viên trung bình (trả lời
các câu hỏi), 5 sinh viên trung bình (trả lời ![]() các câu hỏi). Giám khảo chọn ngẫu nhiên một sinh viên vào thi và ra đề gồm 4 câu hỏi (được lấy ngẫu nhiên từ 20 câu hỏi của đề cương ôn tập). Biết sinh viên này trả lời được cả 4 câu hỏi, tính xác suất để sinh viên đó là sinh viên khá.
các câu hỏi). Giám khảo chọn ngẫu nhiên một sinh viên vào thi và ra đề gồm 4 câu hỏi (được lấy ngẫu nhiên từ 20 câu hỏi của đề cương ôn tập). Biết sinh viên này trả lời được cả 4 câu hỏi, tính xác suất để sinh viên đó là sinh viên khá.
Quảng cáo
Trả lời:
Đáp án đúng là B
Phương pháp giải
Công thức Bayes: 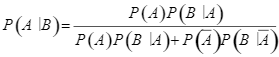 .
.
Lời giải
Gọi ![]() lần lượt là các biến cố "chọn một sinh viên giỏi, khá, trung bình vào thi"
lần lượt là các biến cố "chọn một sinh viên giỏi, khá, trung bình vào thi"
Gọi ![]() là biến cố "sinh viên được chọn vào thi trả lời được cả 4 câu".
là biến cố "sinh viên được chọn vào thi trả lời được cả 4 câu".
Ta có: ![]() .
.
2 sinh viên giỏi trả lời được ![]() các câu hỏi, nên 2 sinh viên này trả lời được cả 20 câu hỏi trong đề cương ôn tập.
các câu hỏi, nên 2 sinh viên này trả lời được cả 20 câu hỏi trong đề cương ôn tập.
3 sinh viên khá trả lời được ![]() các câu hỏi, nên 3 sinh viên này trả lời được
các câu hỏi, nên 3 sinh viên này trả lời được ![]() câu hỏi trong đề cương ôn tập.
câu hỏi trong đề cương ôn tập.
5 sinh viên trung bình trả lời được ![]() các câu hỏi, nên 5 sinh viên này chỉ trả lời được
các câu hỏi, nên 5 sinh viên này chỉ trả lời được ![]() câu hỏi trong đề cương ôn tập.
câu hỏi trong đề cương ôn tập.
Do đó ![]() ;
; ![]() .
.
Áp dụng công thức xác suất toàn phần:
![]()
Xác suất để sinh viên được chọn vào thi là sinh viên khá, biết sinh viên đó trả lời được cả 4 câu hỏi là 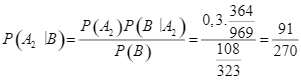
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là C
Phương pháp giải
Vận dụng công thức tính nhiệt lượng: Q = mcΔt
Lời giải
Gọi:
+ m1, V1, t1 là khối lượng, thể tích và nhiệt độ ban đầu và của nước trong bình I.
+ m2, V2, t2 là khối lượng, thể tích và nhiệt độ ban đầu của nước trong bình II.
+ m,V là khối lượng và thể tích nước của mỗi lần rót.
+ t là nhiệt độ cân bằng của bình II sau khi đã rót nước từ bình I sang bình II.
+ t′ là nhiệt độ cân bằng của bình I sau khi đã rót nước từ bình II sang bình I.
- Các phương trình cân bằng nhiệt:
- Vì khối lượng m của nước tỉ lệ với thể tích V nên ta có:
- Giải hệ (1) và (2) ta được:
Vậy: Lượng nước đã rót từ bình này sang bình kia là .
Câu 2
Lời giải
Đáp án đúng là C
Phương pháp giải
Cho ![]() và
và ![]() là hai biến cố, trong đó
là hai biến cố, trong đó ![]() . Khi đó
. Khi đó ![]() .
.
Lời giải
Gọi ![]() là biến cố "người được chọn ra không nhiễm bệnh".
là biến cố "người được chọn ra không nhiễm bệnh".
Và ![]() là biến cố "người được chọn ra không có phản ứng dương tính"
là biến cố "người được chọn ra không có phản ứng dương tính"
Theo bài ta có: ![]() .
.
Do đó: ![]() .
.
Xác suất để người được chọn ra không nhiễm bệnh và không có phản ứng dương tính là
![]() .
.
Câu 3
A. Chiến dịch Biên giới Thu Đông
B. Chiến dịch Điện Biên Phủ
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Biểu hiện về mối quan hệ cha con gần gũi, không thể tách rời
B. Khẳng định vai trò vĩ đại và ý nghĩa của cha trong cuộc đời con
C. Thể hiện tình cảm biết ơn của người con dành cho cha
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. khai thác thêm các mỏ dầu mới, hợp tác quốc tế, lao động ở trong nước đông.
C. khai thác nhiều mỏ dầu, tăng cường hợp tác với nước ngoài, đầu tư công nghệ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.