B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Một số tự nhiên gồm hai chữ số có tổng bằng \[12.\] Nếu đổi chỗ hai chữ số đo cho nhau thì ta được một số mới bé hơn số ban đầu là 18 đơn vị. tìm số ban đầu.
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Một số tự nhiên gồm hai chữ số có tổng bằng \[12.\] Nếu đổi chỗ hai chữ số đo cho nhau thì ta được một số mới bé hơn số ban đầu là 18 đơn vị. tìm số ban đầu.
Quảng cáo
Trả lời:
Gọi \[x\] là chữ số có hàng chục của số cần tìm \[\left( {x \in \mathbb{N},0 < x \le 9} \right)\].
Khi đó chữ số hàng đơn vị là: \[12 - x.\]
Độ lớn số ban đầu là: \[10x + \left( {12 - x} \right)\].
Khi đổi chỗ hai chữ số đó cho nhau thì số mới có chữ số hàng chục là \[12 - x\] và chữ số hàng đơn vị là \[x\]. Số mới có độ lớn là: \[10\left( {12 - x} \right) + x.\]
Sau khi đổi chỗ thì số mới bé hơn số ban đầu là \[18\] đơn vị nên ta có phương trình:
\[\left[ {10x + \left( {12 - x} \right)} \right] - \left[ {10\left( {12 - x} \right) + x} \right] = 18\]
\[10x + 12 - x - 120 + 10x - x = 18\]
\[10x - x + 10x - x = 18 - 12 + 120\]
\[18x = 126\]
\[x = 7\] (thỏa mãn)
Khi đó, số cần tìm có chữ số hàng chục là 7 và chữ số hàng đơn vị là \[12 - 7 = 5\].
Vậy số cần tìm là \[75.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(360\)
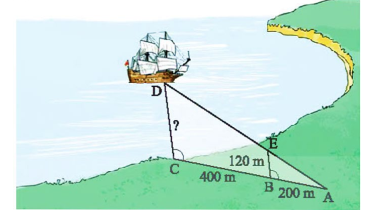
Ta có: \(\widehat {ACD} = \widehat {ABE}\), mà hai góc ở vị trí đồng vị nên \(CD\parallel BE.\)
Ta có: \(AC = AB + BC = 200 + 400 = 600{\rm{ }}\left( {\rm{m}} \right)\).
Theo hệ quả định lí Thalès, ta có: \(\frac{{CD}}{{BE}} = \frac{{AC}}{{AB}}.\)
Hay \(\frac{{CD}}{{120}} = \frac{{600}}{{200}}\) suy ra \(CD = \frac{{600.120}}{{200}} = 360{\rm{ }}\left( {\rm{m}} \right)\).
Lời giải
Đáp án: \(0,14\)
Các kết quả có thể xảy ra khi gieo hai con xúc xắc là \(6.6 = 36\).
Các kết quả thuận lợi cho biến cố “Tổng số chấm sau hai lần gieo bằng 8” là: \(\left( {2;6} \right);\left( {6;2} \right);\left( {3;5} \right);\)\(\left( {5;3} \right);\left( {4;4} \right)\).
Do đó, có 5 kết quả thuận lợi cho biến cố \(B.\)
Suy ra, xác suất của biến cố \(B\) là: \(P\left( B \right) = \frac{5}{{36}} \approx 0,14\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.