(1,5 điểm) Cho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\), đường cao \(AD{\rm{ }}\left( {D \in BC} \right)\). Gọi \(E,F\) lần lượt là hình chiếu của \(D\) trên \(AB\) và \(AC\).
a) Chứng minh \(AE.AB = A{D^2} = AF.AC\) và \(\widehat {AFE} = \widehat {ABC}\).
(1,5 điểm) Cho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\), đường cao \(AD{\rm{ }}\left( {D \in BC} \right)\). Gọi \(E,F\) lần lượt là hình chiếu của \(D\) trên \(AB\) và \(AC\).
a) Chứng minh \(AE.AB = A{D^2} = AF.AC\) và \(\widehat {AFE} = \widehat {ABC}\).
Quảng cáo
Trả lời:
Xét \(\Delta AED\) và \(\Delta ADB\) có:
\(\widehat A\) chung
\(\widehat {AED} = \widehat {ADB} = 90^\circ \)
Suy ra (g.g)
Suy ra \(\frac{{AE}}{{AD}} = \frac{{AD}}{{AB}}\), suy ra \(AE.AB = A{D^2}\) (1)
Xét \(\Delta AFD\) và \(\Delta ADC\) có:
\(\widehat A\) chung
\(\widehat {AFD} = \widehat {ADC} = 90^\circ \) (gt)
Suy ra (g.g)
Suy ra \(\frac{{AF}}{{AD}} = \frac{{AD}}{{AC}}\) suy ra \(AF.AC = A{D^2}\) (2)
Từ (1) và (2) suy ra \(AE.AB = A{D^2} = AF.AC.\)
Do đó, \(\frac{{AE}}{{AF}} = \frac{{AC}}{{AB}}\).
Xét \(\Delta AEF\) và \(\Delta ACB\)có:
\(\widehat A\) chung
\(\frac{{AE}}{{AF}} = \frac{{AC}}{{AB}}\) (cmt)
Suy ra (c.g.c)
Suy ra \(\widehat {AEF} = \widehat {ACB}\).
Câu hỏi cùng đoạn
Câu 2:
b) Gọi \(I\) là giao điểm của \(FE\) và tia \(CB\). Chứng minh \(I{D^2} = IE.IF\).
b) Gọi \(I\) là giao điểm của \(FE\) và tia \(CB\). Chứng minh \(I{D^2} = IE.IF\).
Vì (cmt) suy ra \(\widehat {AEF} = \widehat {ACB}\).
Mà \(\widehat {AEF} = \widehat {IEB}\) (2 góc đối đỉnh)
Suy ra \(\widehat {ACB} = \widehat {IEB}\) (3)
Ta có: \(\widehat {IDF} = \widehat {DFC} + \widehat {ACB}\) (góc ngoài tam giác \(DFC\))
Suy ra \(\widehat {IDF} = 90^\circ + \widehat {ACB}\) (4)
Và \(\widehat {IED} = \widehat {IEB} + \widehat {BED} = \widehat {IEB} + 90^\circ \) (5)
Từ (3), (4), (5) suy ra \(\widehat {IDF} = \widehat {IED}\).
Xét \(\Delta IED\) và \(\Delta IDF\) có:
\(\widehat I\) chung
\(\widehat {IED} = \widehat {IDF}\) (cmt)
Suy ra (g.g)
Suy ra \(\frac{{IE}}{{ID}} = \frac{{ID}}{{IF}}\) nên \(I{D^2} = IE.IF\) (đpcm)
Câu 3:
c) Gọi \(H\) là trực tâm của \(\Delta ABC,\) tia \(HB\) cắt \(EF\) tại \(K.\) Chứng minh \(DK \bot BH.\)
c) Gọi \(H\) là trực tâm của \(\Delta ABC,\) tia \(HB\) cắt \(EF\) tại \(K.\) Chứng minh \(DK \bot BH.\)
Vì \(H\) là trực tâm của \(\Delta ABC\) nên \(BH \bot AC\).
Mà \(DF \bot AC\) nên \(BH\parallel DF\), suy ra \(\widehat {EFD} = \widehat {EKB}\) (hai góc đồng vị) (6)
Theo câu b) ta có nên \(\widehat {IDE} = \widehat {IFD}\) suy ra \(\widehat {BDE} = \widehat {EFD}\) (7)
Từ (6) và (7) suy ra \(\widehat {EKB} = \widehat {BDE}\).
Gọi \(L\) là giao điểm của \(BK\) và \(ED\).
Xét \(\Delta EKL\) và \(\Delta BDL\) có:
\(\widehat {EKL} = \widehat {LDB}\) (cmt)
\(\widehat {ELK} = \widehat {DLB}\) (đối đỉnh)
Suy ra (g.g)
Suy ra \(\frac{{EL}}{{LB}} = \frac{{KL}}{{LD}}\).
Xét \(\Delta EBL\) và \(\Delta KDL\) có: \(\frac{{EL}}{{LB}} = \frac{{KL}}{{LD}}\) (cmt) và \(\widehat {ELB} = \widehat {DLK}\) (2 góc đối đỉnh)
Suy ra (g.g)
Suy ra \(\widehat {DKL} = \widehat {BEL} = 90^\circ \) hay \(DK \bot BH\) tại \(K\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(360\)
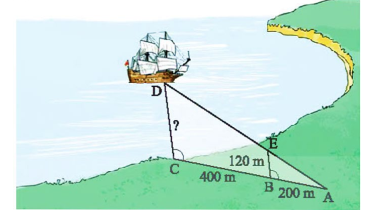
Ta có: \(\widehat {ACD} = \widehat {ABE}\), mà hai góc ở vị trí đồng vị nên \(CD\parallel BE.\)
Ta có: \(AC = AB + BC = 200 + 400 = 600{\rm{ }}\left( {\rm{m}} \right)\).
Theo hệ quả định lí Thalès, ta có: \(\frac{{CD}}{{BE}} = \frac{{AC}}{{AB}}.\)
Hay \(\frac{{CD}}{{120}} = \frac{{600}}{{200}}\) suy ra \(CD = \frac{{600.120}}{{200}} = 360{\rm{ }}\left( {\rm{m}} \right)\).
Lời giải
Đáp án: \(0,14\)
Các kết quả có thể xảy ra khi gieo hai con xúc xắc là \(6.6 = 36\).
Các kết quả thuận lợi cho biến cố “Tổng số chấm sau hai lần gieo bằng 8” là: \(\left( {2;6} \right);\left( {6;2} \right);\left( {3;5} \right);\)\(\left( {5;3} \right);\left( {4;4} \right)\).
Do đó, có 5 kết quả thuận lợi cho biến cố \(B.\)
Suy ra, xác suất của biến cố \(B\) là: \(P\left( B \right) = \frac{5}{{36}} \approx 0,14\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.