Câu hỏi:
17/03/2025 135
(1,5 điểm) Cho hình bình hành \(ABCD\), điểm \(F\) trên cạnh \(BC\). Tia \(AF\) cắt \(BD\) và \(DC\) lần lượt ở \(E\) và \(G\). Chứng minh rằng:
(1,5 điểm) Cho hình bình hành \(ABCD\), điểm \(F\) trên cạnh \(BC\). Tia \(AF\) cắt \(BD\) và \(DC\) lần lượt ở \(E\) và \(G\). Chứng minh rằng:
a) và
Quảng cáo
Trả lời:
Giải bởi Vietjack
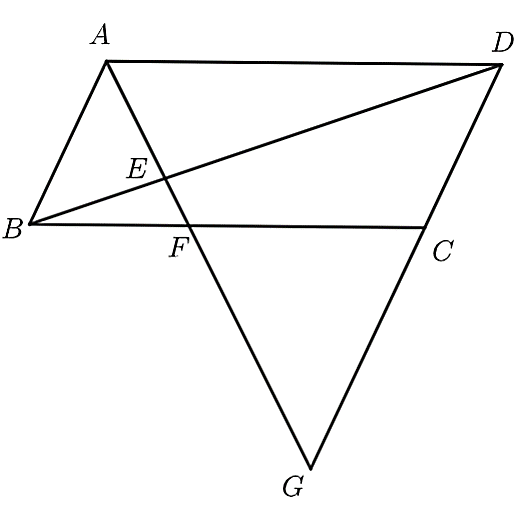
Ta có: \(BF\parallel AD\) (gt)
Suy ra \(\widehat {EDA} = \widehat {EBF}\) (so le trong)
\(\widehat {EAD} = \widehat {EFB}\) (so le trong)
Xét \(\Delta DEA\) và \(\Delta BEF\), có:
\(\widehat {EDA} = \widehat {EBF}\) (so le trong)
\(\widehat {EAD} = \widehat {EFB}\) (so le trong)
Do đó, (g.g)
Lại có \(AB\parallel GD\) (gt) nên \(\widehat {DGE} = \widehat {BAE}\) (so le trong)
Xét \(\Delta DGE\) và \(\Delta BAE\), có:
\(\widehat {DGE} = \widehat {BAE}\) (so le trong)
\(\widehat {DEG} = \widehat {BEA}\) (đối đỉnh)
Suy ra (g.g)
Câu hỏi cùng đoạn
Câu 2:
b) \(A{E^2} = EF.EG\).
b) \(A{E^2} = EF.EG\).
Lời giải của GV VietJack
Ta có: (cmt) nên \[\frac{{AE}}{{EF}} = \frac{{DE}}{{BE}}\] (1)
(cmt) nên \[\frac{{GE}}{{EA}} = \frac{{DE}}{{BE}}\] (2)
Từ (1) và (2) suy ra \[\frac{{GE}}{{EA}} = \frac{{AE}}{{FE}}\] nên \(A{E^2} = EF.EG\) (đpcm).
Câu 3:
c) \(BF.DG\) không đổi khi \(F\) thay đổi trên \(BC.\)
c) \(BF.DG\) không đổi khi \(F\) thay đổi trên \(BC.\)
Lời giải của GV VietJack
Từ câu a), ta có: nên \[\frac{{AD}}{{BF}} = \frac{{DE}}{{BE}}\] (3)
nên \[\frac{{GD}}{{BA}} = \frac{{DE}}{{BE}}\] (4)
Từ (3) và (4) suy ra \[\frac{{GD}}{{BA}} = \frac{{DA}}{{BF}}\] nên \[BF.DG = AD.BA\].
Do \(ABCD\) là hình bình hành nên \[AD.BA\] không đổi.
Do đó, \[BF.DG\] không đổi khi \[F\] thay đổi trên \[BC.\]
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: B
Ta có đồ thị hàm số \(y = 2x + 1\) và đồ thị hàm số \(y = ax + 3\) là hai đường thẳng song song do đó hệ số góc của hai đường thẳng bằng nhau và bằng \(2.\)
Vậy \(a = 2.\)
Lời giải
Đáp án: \(1\)
Gọi đường thẳng cần tìm là \(\left( d \right):y = ax + b\).
Ta có: \(A\left( {1;2} \right) \in \left( d \right)\) nên \(a + b = 2\) suy ra \(b = 2 - a\) (1)
\(B\left( {3;4} \right) \in \left( d \right)\) nên \(3a + b = 4\) suy ra \(b = 4 - 3a\) (2)
Từ (1) và (2) ta có: \(2 - a = 4 - 3a\) suy ra \(2a = 2\) nên \(a = 1\).
Vậy hệ số góc của đường thẳng đó là \(1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo