(1,5 điểm) Cho hình chữ nhật \(ABCD\). Kẻ \(AH \bot BD\) tại \(H.\)
a) Chứng minh rằng .
(1,5 điểm) Cho hình chữ nhật \(ABCD\). Kẻ \(AH \bot BD\) tại \(H.\)
a) Chứng minh rằng .
Quảng cáo
Trả lời:
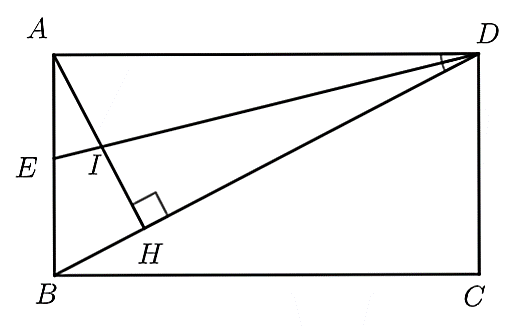
Vì \(ABCD\) là hình chữ nhật nên \(\widehat {BAD} = 90^\circ \).
Vì \(AH \bot BD\) tại \(H\) nên \(\widehat {BAD} = \widehat {AHB} = 90^\circ \).
Xét \(\Delta ABD\) và \(\Delta HBA\), có:
\(\widehat {BAD} = \widehat {AHB} = 90^\circ \) (cmt)
\(\widehat {ABD} = \widehat {ABH}\)
Do đó, (g.g)
Câu hỏi cùng đoạn
Câu 2:
b) Chứng minh rằng \(B{C^2} = BD.DH.\)
b) Chứng minh rằng \(B{C^2} = BD.DH.\)
Xét \(\Delta ABD\) và \(\Delta HAD\) có:
\(\widehat {BAD} = \widehat {AHD} = 90^\circ \)
\(\widehat {BDA} = \widehat {ADH}\)
Do đó, (g.g)
Suy ra \(\frac{{AD}}{{DH}} = \frac{{BD}}{{AD}}\) hay \[A{D^2} = BD.DH\].
Mà \[AD = BC\] (do \[ABCD\] là hình chữ nhật)
Suy ra \[B{C^2} = BD.DH\] (đpcm)
Câu 3:
c) Kẻ \(DE\) là đường phân giác của tam giác \(ABD\). Gọi \(I\) là giao điểm của \(DE\) và \(AH\). Chứng minh \(\Delta AIE\) cân và \(A{E^2} = IH.EB.\)
c) Kẻ \(DE\) là đường phân giác của tam giác \(ABD\). Gọi \(I\) là giao điểm của \(DE\) và \(AH\). Chứng minh \(\Delta AIE\) cân và \(A{E^2} = IH.EB.\)
Vì \(DE\) là đường phân giác của tam giác \(ABD\) nên \(\widehat {ADE} = \widehat {EDB}\).
Ta có: (cmt) nên \(\widehat {DBA} = \widehat {HAD}\) (hai góc tương ứng)
Suy ra \(\widehat {DBA} + \widehat {EDB} = \widehat {HAD} + \widehat {EDA}\) (1)
Xét \(\Delta AID\) có \(\widehat {AIE} = \widehat {IAD} + \widehat {IDA} = \widehat {HAD} + \widehat {EDA}\) (tính chất góc ngoài) (2)
Xét \(\Delta DEB\) có \(\widehat {AEI} = \widehat {EBD} + \widehat {BDE}\) (tính chất góc ngoài ) (3)
Từ (1), (2), (3) suy ra \(\widehat {AIE} = \widehat {AEI}\).
Do đó, \(\Delta AIE\) cân tại \(A\).
Suy ra \(AE = AI\).
Xét \(\Delta ADH\), có \(DI\) là đường phân giác nên \(\frac{{IH}}{{IA}} = \frac{{DH}}{{DA}}.\)
Mà \(AE = AI\) (cmt) (4)
Suy ra \(\frac{{AD}}{{DH}} = \frac{{BD}}{{AD}}\), suy ra \(\frac{{AD}}{{BD}} = \frac{{DH}}{{DA}}\) (5)
Từ (4) và (5) suy ra \(\frac{{IH}}{{EA}} = \frac{{AD}}{{BD}}\) \(\left( * \right)\)
Xét \(\Delta ADB\) có \(DE\) là đường phân giác nên \(\frac{{AE}}{{EB}} = \frac{{AD}}{{BD}}\)\(\left( {**} \right)\)
Từ (*) và (**) suy ra \(\frac{{IH}}{{EA}} = \frac{{AE}}{{EB}}\) hay \(A{E^2} = IH.EB\) (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đặt \(a = 2024 - x;{\rm{ }}b = 2026 - x;{\rm{ }}c = 2x - 4050\).
Ta có: \(a + b + c = 2024 - x + 2026 - x + 2x - 4050 = 0\)
Suy ra \(\left( {a + b} \right) = - c\) nên \({\left( {a + b} \right)^3} = - {c^3}\).
Khi đó, \({a^3} + {b^3} + {c^3} = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right) + {c^3} = - {c^3} + 3abc + {c^3} = 3abc\).
Do đó, \({\left( {2024 - x} \right)^3} + {\left( {2026 - x} \right)^3} + {\left( {2x - 4050} \right)^3} = 0\)
\(3\left( {2024 - x} \right)\left( {2026 - x} \right)\left( {2x - 4050} \right) = 0\)
Suy ra \(2024 - x = 0\) hoặc \(2026 - x = 0\) hoặc \(2x - 4050 = 0\).
Do đó, \(x = 2024\) hoặc \(x = 2026\) hoặc \(x = 2025\).
Vậy nghiệm của phương trình đã cho là \(S = \left\{ {2024;2025;2026} \right\}\).
Lời giải
Đúng
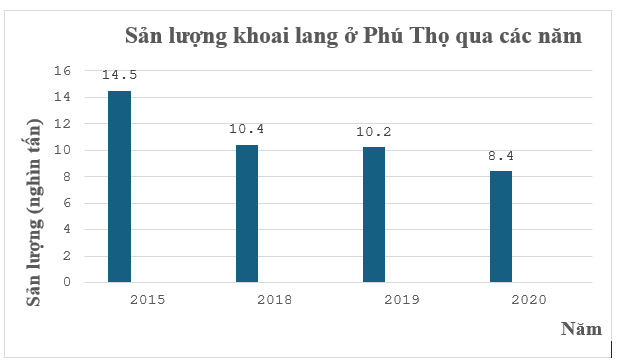
a) Cửa hàng đã thu thập dữ liệu biểu diễn trong biểu đồ bằng phương pháp phỏng vấn \(1{\rm{ }}000\) khách hàng. Đây là phương pháp thu thập trực tiếp.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.