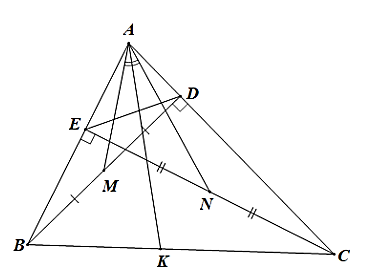
(1,5 điểm) Cho tam giác \(ABC\) có ba góc nhọn \(\left( {AB < AC} \right)\), vẽ các đường cao \(BD\) và \(CE\).
a) Chứng minh rằng .
(1,5 điểm) Cho tam giác \(ABC\) có ba góc nhọn \(\left( {AB < AC} \right)\), vẽ các đường cao \(BD\) và \(CE\).
a) Chứng minh rằng .
Quảng cáo
Trả lời:
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(\widehat {BAC}\) chung (gt)
\(\widehat {ADB} = \widehat {AEC} = 90^\circ \) (gt)
Suy ra (g.g).
Câu hỏi cùng đoạn
Câu 2:
b) Chứng minh rằng \(\widehat {ABC} + \widehat {EDC} = 180^\circ \).
b) Chứng minh rằng \(\widehat {ABC} + \widehat {EDC} = 180^\circ \).
Vì (cmt) nên \(\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}\) (các cặp tương ứng tỉ lệ)
Xét \(\Delta AED\) và \(\Delta ACB\) có:
\(\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}\) (cmt)
\(\widehat {BAC}\) chung
Do đó, (c.g.c)
Suy ra \(\widehat {ADE} = \widehat {ABC}\) (hai góc tương ứng)
Mặt khác \(\widehat {ADE} + \widehat {EDC} = 180^\circ \) (hai góc kề bù)
Do đó, \(\widehat {ADE} + \widehat {EDC} = \widehat {ABC} + \widehat {EDC} = 180^\circ \).
Câu 3:
c) Gọi \(M,N\) lần lượt là trung điểm của đoạn thẳng \(BD\) và \(CE\). Vẽ \(AK\) là phân giác ngoài của \(\widehat {MAN}\) \(\left( {K \in BC} \right)\). Chứng minh rằng \(KB.AC = KC.AB.\)
c) Gọi \(M,N\) lần lượt là trung điểm của đoạn thẳng \(BD\) và \(CE\). Vẽ \(AK\) là phân giác ngoài của \(\widehat {MAN}\) \(\left( {K \in BC} \right)\). Chứng minh rằng \(KB.AC = KC.AB.\)
Vì nên \(\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}\).
Mà \(M,N\) lần lượt là trung điểm của đoạn thẳng \(BD\) và \(CE\) nên \(BD = 2BM\) và \(CE = 2CN.\)
Suy ra \(\frac{{AB}}{{AC}} = \frac{{BD}}{{CE}} = \frac{{2BM}}{{2CN}} = \frac{{BM}}{{CN}}.\)
Xét \(\Delta ABD\) và \(\Delta ACN\) có: \(\frac{{BM}}{{CN}} = \frac{{AB}}{{AC}}\) (cmt)
\(\widehat {ABM} = \widehat {ACN}\) (cùng phụ với \(\widehat {BAC}\))
Do đó, (c.g.c)
Suy ra \(\widehat {BAM} = \widehat {CAN}\) (hai góc tương ứng)
Lại có \(AK\) là tia phân giác của \(\widehat {MAN}\) (giả thiết)
Suy ra \(\widehat {KAM} = \widehat {KAN}\) (tính chất tia phân giác của một góc)
Do đó, \(\widehat {KAM} + \widehat {BAM} = \widehat {KAN} + \widehat {CAN}\) hay \(\widehat {BAK} = \widehat {KAC}\).
Nên \(AK\) là tia phân giác của \(\widehat {BAC}\).
Theo tính chất tia phân giác của tam giác, ta có: \(\frac{{AB}}{{AC}} = \frac{{KB}}{{KC}}\).
Do đó, \(KB.AC = KC.AB\) (điều phải chứng minh).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(50\)
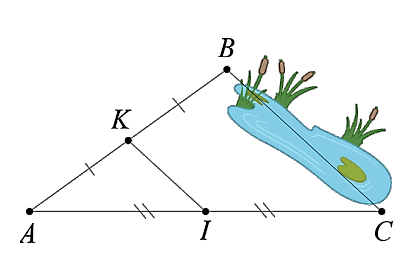
Xét tam giác \(ABC\) có \(K\) là trung điểm của \(AB\); \(I\) là trung điểm của \(AC\).
Do đó, \(KI\) là đường trung bình của tam giác \(ABC\).
Suy ra \(KI = \frac{1}{2}BC\) hay \(BC = 2KI = 50{\rm{ }}\left( {\rm{m}} \right)\).
Vậy độ dài của \(BC\) bằng \(50{\rm{ m}}{\rm{.}}\)
Lời giải
Đúng
Ta có biểu đồ đã cho là biểu đồ đoạn thẳng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.