Câu 9-11. Cho đường tròn \(\left( {O;\,\,R} \right)\). Từ \(A\) trên \(\left( O \right),\) kẻ tiếp tuyến \(d\) với \(\left( O \right).\) Trên đường thẳng \(d\) lấy điểm \(M\) bất kỳ \(\left( M \right.\) khác \(\left. A \right),\) kẻ cát tuyến \(MNP.\) Gọi \(K\) là trung điểm của \(NP,\) kẻ tiếp tuyến \(MB.\) Kẻ \[AC \bot MB,\,\,BD \bot AM\,\,\left( {C \in MB,\,\,D \in AM} \right).\] Gọi\[H\] là giao điểm của \[AC\] và \[BD,\] \[I\] là giao điểm của \[OM\] và \[AB.\]
a) Chứng minh tứ giác \(AMBO\) nội tiếp.
Câu 9-11. Cho đường tròn \(\left( {O;\,\,R} \right)\). Từ \(A\) trên \(\left( O \right),\) kẻ tiếp tuyến \(d\) với \(\left( O \right).\) Trên đường thẳng \(d\) lấy điểm \(M\) bất kỳ \(\left( M \right.\) khác \(\left. A \right),\) kẻ cát tuyến \(MNP.\) Gọi \(K\) là trung điểm của \(NP,\) kẻ tiếp tuyến \(MB.\) Kẻ \[AC \bot MB,\,\,BD \bot AM\,\,\left( {C \in MB,\,\,D \in AM} \right).\] Gọi\[H\] là giao điểm của \[AC\] và \[BD,\] \[I\] là giao điểm của \[OM\] và \[AB.\]
Câu hỏi trong đề: Bộ 5 đề thi cuối kì 2 Toán 9 Cánh diều (Tự luận) có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
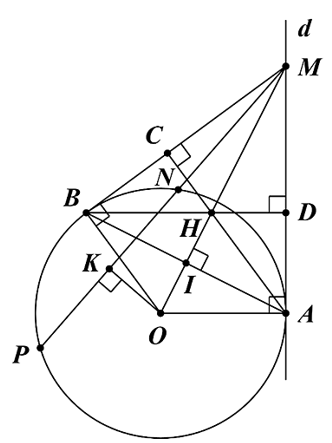
a) Ta có \(\widehat {OAM} = 90^\circ \) (do \[MA\] là tiếp tuyến của \[\left( O \right)\], \[A\] là tiếp điểm).
Suy ra ba điểm \(O,\,\,A,\,\,M\) cùng thuộc một đường tròn đường kính
Lại có \(\widehat {OBM} = 90^\circ \) (do \[MB\] là tiếp tuyến của \[\left( O \right)\], \[B\] là tiếp điểm).
Suy ra ba điểm \(O,\,\,B,\,\,M\) cùng thuộc một đường tròn đường kínhTừ \[\left( 1 \right)\] và \[\left( 2 \right)\] ta được tứ giác \[AMBO\] nội tiếp đường tròn đường kính \[OM.\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] ta được tứ giác \[AMBO\] nội tiếp đường tròn đường kính \[OM.\]
Câu hỏi cùng đoạn
Câu 2:
b) Chứng minh \(OI \cdot OM = {R^2}\).
Giải bởi Vietjack
b) Ta có tứ giác \[AMBO\] nội tiếp đường tròn đường kính \[OM.\]
Suy ra \[AB\] là dây cung của đường tròn đường kính \[OM.\]
Do đó \(OM \bot AB\).
Xét \(\Delta OAM\) vuông tại \[A\] có \[AI\] là đường cao.
Xét \(\Delta OAM\) và \[\Delta OIA\] là hai tam giác vuông có góc \[\widehat O\] chung.
Do đó
Suy ra \[\frac{{OA}}{{OI}} = \frac{{OM}}{{OA}}\] hay \[O{A^2} = OM.OI\] mà \[OA = R\] nên \(OI \cdot OM = {R^2}\).
Câu 3:
c) Chứng minh ba điểm \(O,\,\,H,\,\,M\) thẳng hàng.
Giải bởi Vietjack
c) Áp dụng định lí Pythagore trong tam giác vuông \[IOA\], ta có
\[I{A^2} = O{A^2} - O{I^2} = OI \cdot OM - O{I^2} = OI\left( {OM - OI} \right) = OI \cdot IM\].
Ta có \(OA \bot AM\) (do \[AM\] là tiếp tuyến của \(\left( O \right)\) và \(BD \bot MA\) (gt), suy ra \[OA\,{\rm{//}}\,BD\].
Chứng minh tương tự, ta được \[OB\,\,{\rm{//}}\,AC\].
Do đó tứ giác \[OAHB\] là hình bình hành.
Mà \(OA = OB = R\) nên tứ giác \[OAHB\] là hình thoi, suy ra \(OH \bot AB\).
Mà \(OM \bot AB\), do đó \[OM \equiv OH\].
Vậy ba điểm \[O,\,\,H,M\] thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Từ biểu đồ trên, ta có bảng tần số ghép nhóm tương ứng như sau:
|
Cân nặng (kg) |
\[\left[ {35\,;\,\,40} \right)\] |
\[\left[ {40\,;\,\,45} \right)\] |
\[\left[ {45\,;\,\,50} \right)\] |
\[\left[ {50\,;\,\,55} \right)\] |
\[\left[ {55\,;\,\,60} \right)\] |
\[\left[ {60\,;\,\,65} \right)\] |
|
Tần số tương đối |
5% |
10% |
37,5% |
27,5% |
15% |
5% |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có một bát giác đều \(ABCDEFGH\) nội tiếp trong đường tròn \(\left( O \right)\), mỗi góc ở tâm là: \(360^\circ :8 = 45^\circ .\)
Theo giả thiết, ta có: \(\widehat {AOD} = 3 \cdot 45^\circ = 135^\circ .\;\)
Vậy qua phép quay thuận chiểu \(135^\circ \) tâm \(O\), cabin \(A\) di chuyển đến vị trí cao nhất (điểm \(D).\)Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập