(0,5 điểm) Bạn Tú có một hộp bút trong đó có \[5\] chiếc bút bi mực xanh, \[7\]chiếc bút bi mực đen và \[3\] chiếc bút chì. Bạn lấy ngẫu nhiên hai chiếc bút. Tính xác suất của biến cố: “Bạn Tú lấy được \(1\) chiếc bút chì và \(1\) chiếc bút mực”.
(0,5 điểm) Bạn Tú có một hộp bút trong đó có \[5\] chiếc bút bi mực xanh, \[7\]chiếc bút bi mực đen và \[3\] chiếc bút chì. Bạn lấy ngẫu nhiên hai chiếc bút. Tính xác suất của biến cố: “Bạn Tú lấy được \(1\) chiếc bút chì và \(1\) chiếc bút mực”.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chiếc bút thứ nhất chọn \[1\] trong số \[15\] chiếc bút nên có \[15\] cách.
Chiếc bút thứ hai chọn \[1\] trong \[14\] chiếc bút còn lại nên có \[14\] cách.
Số cách chọn \[2\] chiếc bút là \[\frac{{15 \cdot 14}}{2} = 105\] (cách) (cứ mỗi cặp bị lăp lại 2 lần).
Chiếc bút chì chọn \[1\] trong \[3\] chiếc nên có 3 cách.
Chiếc thứ hai chọn \[1\] trong \[12\] chiếc bút mực nên có \[12\] cách.
Số cách chọn ra \(2\) chiếc bút trong đó có \(1\) chiếc bút chì và một chiếc bút mực là \[3 \cdot 12 = 36\] (cách).
Xác suất của biến cố: “Bạn Tú lấy được \(1\) chiếc bút chì và \(1\) chiếc bút mực” là \(\frac{{36}}{{105}} = \frac{{12}}{{35}}\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
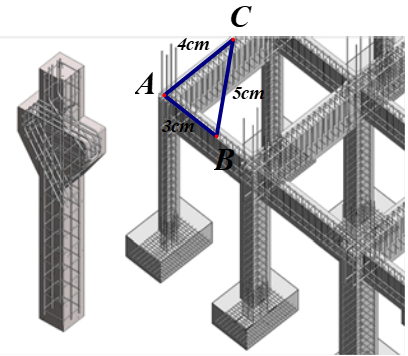
Xét tam giác \[ABC\] ta có:
\(B{C^2} = {5^2} = 25;\) \(A{B^2} + A{C^2} = {3^2} + {4^2} = 25\)
Do đó \(B{C^2} = A{B^2} + A{C^2}.\)
Theo định lý Pythagore đảo thì tam giác \[ABC\] vuông tại \[A.\]
Vậy hai phần móng đó vuông góc với nhau.Lời giải
a) Công thức để chuyển đổi \(x\) euro sang \(y\) đô la Mỹ là \[y = 1,1052x\].
Công thức tính \(y\) theo \(x\) này là hàm số bậc nhất của \(x\) vì với mỗi giá trị của \(x\), ta xác định duy nhất một giá trị của \(y\).
b) 200 euro có giá trị là \[1,1052 \cdot 200 = 210,4\] đô la Mỹ.
500 đô la Mỹ có giá trị là \[500:1,1052 \approx 475,3\] euro.
Vậy vào ngày đó, 200 euro có giá trị bằng khoảng 210,4 đô la Mỹ; 500 đô la Mỹ có giá trị bằng khoảng 475,3 euro.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập