Có hai túi I và II mỗi túi chứa 5 tấm thẻ được đánh số \(1;2;3;4;5\). Rút ngẫu nhiên từ mỗi túi ra một tấm thẻ và nhân hai số ghi trên tấm thẻ với nhau. Tính xác suất của biến cố \(A\): “Kết quả là \(1\) hoặc một số nguyên tố”. (Kết quả ghi dưới dạng số thập phân)
Có hai túi I và II mỗi túi chứa 5 tấm thẻ được đánh số \(1;2;3;4;5\). Rút ngẫu nhiên từ mỗi túi ra một tấm thẻ và nhân hai số ghi trên tấm thẻ với nhau. Tính xác suất của biến cố \(A\): “Kết quả là \(1\) hoặc một số nguyên tố”. (Kết quả ghi dưới dạng số thập phân)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: \(0,28\)
Số phần tử không gian mẫu là: \(5.5 = 25\).
Trường hợp 1: Tích hai số là 1 thì hai thẻ rút ra đều ghi số 1.
Do đó, có 1 kết quả có thể xảy ra.
Trường hợp 2: Tích hai số là số nguyên tố.
Các kết quả có thể xảy ra là: \(\left( {1;2} \right);{\rm{ }}\left( {1;3} \right);{\rm{ }}\left( {1;5} \right);{\rm{ }}\left( {2;1} \right);{\rm{ }}\left( {3;1} \right);{\rm{ }}\left( {5;1} \right)\).
Do đó, có 6 kết quả có thể xảy ra.
Suy ra \(n\left( A \right) = 1 + 6 = 7\).
Vậy xác suất của biến cố \(A\) là: \(P\left( A \right) = \frac{7}{{25}} = 0,28\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\frac{{2x + 1}}{{x - 3}}.\)
B. \(\frac{{\sqrt x }}{{x - 3}}.\)
C. \(\frac{{\sqrt {2x} + 1}}{{x - 3}}.\)
D. \(\frac{{2x + 1}}{{\sqrt {x - 3} }}.\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Phân thức đại số là một biểu thức có dạng \(\frac{A}{B}\) trong đó \(A,B\) là hai đa thức và đa thức \(B \ne 0\).
Do đó, \(\frac{{2x + 1}}{{x - 3}}\) là một phân thức đại số.
Lời giải
Hướng dẫn giải
Đáp án: \(9\)
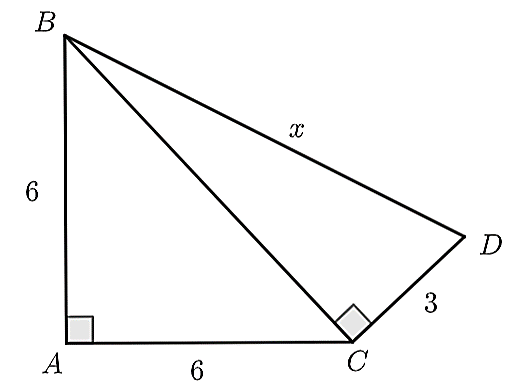
Áp dụng định lí Pythagore vào tam giác \(ABC\), ta có:
\(A{B^2} + A{C^2} = B{C^2}\) hay \({6^2} + {6^2} = B{C^2}\) nên \(B{C^2} = 72\), suy ra \(BC = \sqrt {72} \).
Áp dụng định lí Pythagore vào tam giác \(BCD\), ta có:
\(B{C^2} + C{D^2} = B{D^2}\) hay \({\left( {\sqrt {72} } \right)^2} + {3^2} = {x^2}\) nên \({x^2} = 81\), suy ra \(x = 9\).
Vậy \(x = 9\).
Câu 3
A. \(2x - 2023 = 0.\)
B. \(3x = 0.\)
C. \(2x + \sqrt 3 = 0.\)
D. \(\left( {x - 2} \right)\left( {x + 2} \right) = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Có tung độ bằng \(1,\) hoành độ bằng \(0.\)
B. Có hoành độ bằng \(1,\) tung độ bằng \(0.\)
C. Có hoành độ bằng \(1,\) tung độ bằng \(1.\)
D. Có tung độ bằng \(1,\) hoành độ tùy ý.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo