Dựa vào thông tin dưới đây để trả lời các câu từ 85 đến 87
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, \(AB = a,AA' = 2a\), \(A'C = 3a\). Gọi M là trung điểm của đoạn A'C', I là giao điểm của AM và A'C.
Độ dài đường cao kẻ từ đỉnh I của tứ diện \(IABC\) bằng
Dựa vào thông tin dưới đây để trả lời các câu từ 85 đến 87
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, \(AB = a,AA' = 2a\), \(A'C = 3a\). Gọi M là trung điểm của đoạn A'C', I là giao điểm của AM và A'C.
Quảng cáo
Trả lời:
Giải bởi Vietjack
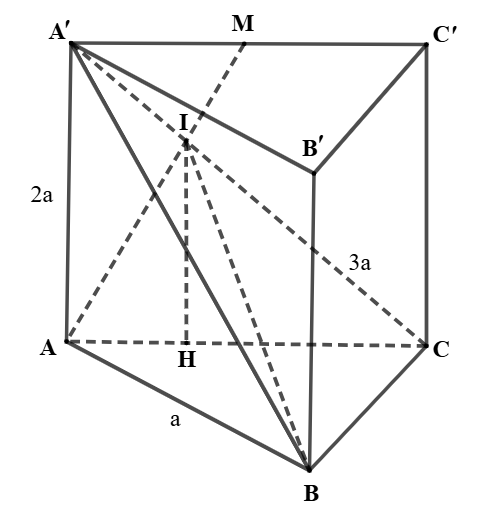
Hạ \[IH \bot AC\,\,\left( {H \in AC} \right) \Rightarrow IH \bot \left( {ABC} \right)\] nên IH là đường cao của tứ diện IABC.
Theo định lí Thalès, ta có \(\frac{{CI}}{{IA'}} = \frac{{AC}}{{A'M}} = \frac{{A'C'}}{{A'M}} = \frac{1}{2}\).
Suy ra \(\frac{{CI}}{{CA'}} = \frac{2}{3}\).
Khi đó, \[\frac{{IH}}{{AA'}} = \frac{{CI}}{{CA'}} = \frac{2}{3} \Rightarrow IH = \frac{2}{3}AA' = \frac{{4a}}{3}\]. Chọn C.Câu hỏi cùng đoạn
Câu 2:
Thể tích khối tứ diện \(IABC\) là:
Giải bởi Vietjack
Ta có \[AC = \sqrt {A'{C^2} - A'{A^2}} = a\sqrt 5 \]; \[BC = \sqrt {A{C^2} - A{B^2}} = 2a\].
Diện tích tam giác ABC: \[{S_{ABC}} = \frac{1}{2}AB \cdot BC = {a^2}\].
Thể tích khối tứ diện IABC: \[V = \frac{1}{3}IH \cdot {S_{ABC}} = \frac{{4{a^3}}}{9}\]. Chọn D.
Câu 3:
Khoảng cách từ điểm A đến mặt phẳng \(\left( {IBC} \right)\) là:
Giải bởi Vietjack
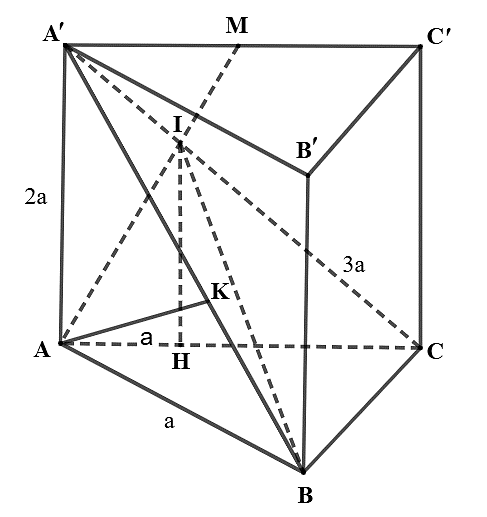
Hạ \[AK \bot A'B\,\,\left( {K \in A'B} \right)\].
Vì \[BC \bot \left( {ABB'A'} \right)\] nên \[AK \bot BC\].
Suy ra \[AK \bot \left( {IBC} \right)\]. Do đó, khoảng cách từ A đến mặt phẳng \(\left( {IBC} \right)\) là AK.
Ta có \[AK = \frac{{2{S_{AA'B}}}}{{A'B}} = \frac{{AA' \cdot AB}}{{\sqrt {A'{A^2} + A{B^2}} }} = \frac{{2a\sqrt 5 }}{5}\]. Chọn A.Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
“Ngào ngạt” có nghĩa là (mùi thơm) bốc lên lan toả rộng và kích thích mạnh vào khứu giác, như vậy chỉ có từ “nồng nàn” mới thể hiện được hương thơm mạnh của thiên nhiên hoa cỏ. Chọn C.
Câu 2
Lời giải
Từ “Thế thái” có thể được hiểu như sau: thế: đời, thái: thói.
Từ “Nhân tình” có thể được hiểu như sau: tình cảm giữa con người với nhau; tình người.
=> Như vậy, “Thế thái – nhân tình” có nghĩa là thói đời và tình người. Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập