PHẦN 1: SỬ DỤNG NGÔN NGỮ

1.1. TIẾNG VIỆT (30 CÂU)

Ngày xưa, Thần Trụ Trời là vị thần khổng lồ, được giao nhiệm vụ xây dựng thế giới. Ngài đã dùng đất đá để đắp thành một trụ lớn, chống đỡ bầu trời và chia cắt trời đất. Khi công việc hoàn thành, Thần Trụ Trời đẩy bầu trời lên cao, tạo nên không gian rộng lớn giữa trời và đất. Sau đó, ngài phá hủy cây trụ để đất đá rơi xuống, hình thành núi non, sông suối, đồng bằng, và biển cả. Từ đó, trời đất trở nên hài hòa, và muôn loài bắt đầu sinh sôi, nảy nở.

(Thần thoại Việt Nam, Thần Trụ Trời)
Theo thần thoại Việt Nam, Thần Trụ Trời đã làm gì để phân chia trời và đất?

A. Sử dụng phép thuật để tạo ra khoảng cách giữa trời và đất.

B. Đắp một trụ lớn để chống đỡ bầu trời và đẩy bầu trời lên cao.

C. Sử dụng nước và gió để hình thành không gian rộng lớn.

D. Dùng sức mạnh để phá hủy núi non và biển cả.

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 23) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Dựa vào câu văn: “Ngài đã dùng đất đá để đắp thành một trụ lớn, chống đỡ bầu trời và chia cắt trời đất.”. Chọn B.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Dựa vào thông tin dưới đây để trả lời các câu từ 70 đến 71

Cho một chất điểm chuyển động theo quy luật vận tốc \[v\left( t \right)\](đơn vị: \[{\rm{m/s}}\]) có đồ thị như hình vẽ bên. Trong đó đồ thị có dạng các đoạn thẳng tương ứng theo thời gian \[t\] giây khi \[0 \le t \le 3\] và \[8 \le t \le 15\], biết \[v\left( t \right)\] có dạng đường Parabol tương ứng thời gian \[t\] giây khi \[3 \le t \le 8\].

Vận tốc trung bình \({v_{tb}}\) của chất điểm trong thời gian \[t\] giây \[\left( {3 \le t \le 8} \right)\] là:

A. \(\frac{{57}}{2}\,\,{\rm{m/s}}\).

B. \(\frac{{23}}{3}\,\,{\rm{m/s}}\).

C. \[11\,\,{\rm{m/s}}\].

D. \(\frac{{115}}{{18}}\,\,{\rm{m/s}}\).

Lời giải

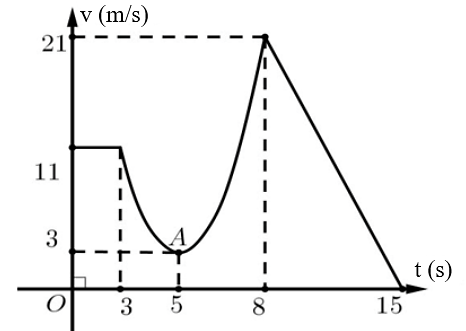
Gọi hàm vận tốc thời gian \(t\) giây \[\left( {3 \le t \le 8} \right)\]có dạng là \(\left( P \right):v\left( t \right) = a{t^2} + bt + c\).

\(\left( P \right)\) đi qua các điểm: \[\left( {3\,;11} \right)\]; \[\left( {5\,;3} \right)\]; \[\left( {8\,;21} \right)\] nên ta có hệ phương trình:

\(\left\{ \begin{array}{l}9a + 3b + c = 11\\25a + 5b + c = 3\\64a + 8b + c = 21\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 20\\c = 53\end{array} \right.\) \( \Rightarrow \left( P \right):v\left( t \right) = 2{t^2} - 20t + 53\).

Quãng đường chất điểm đi được trong thời gian \(t\) giây \[\left( {3 \le t \le 8} \right)\] là:

\(S' = \int\limits_3^8 {\left( {2{t^2} - 20t + 53} \right)\,{\rm{d}}t = \frac{{115}}{3}} \,\,(m)\).

Vận tốc trung bình của chất điểm trong thời gian \[t\] giây \[\left( {3 \le t \le 8} \right)\] là:

\[\frac{{115}}{3}:\left( {8 - 3} \right) = \frac{{23}}{3}\] (\[{\rm{m/s}}\]). Chọn B.

Câu 2

Dựa vào thông tin dưới đây để trả lời các câu từ 70 đến 71

Cho một chất điểm chuyển động theo quy luật vận tốc \[v\left( t \right)\](đơn vị: \[{\rm{m/s}}\]) có đồ thị như hình vẽ bên. Trong đó đồ thị có dạng các đoạn thẳng tương ứng theo thời gian \[t\] giây khi \[0 \le t \le 3\] và \[8 \le t \le 15\], biết \[v\left( t \right)\] có dạng đường Parabol tương ứng thời gian \[t\] giây khi \[3 \le t \le 8\].

Quãng đường mà chất điểm đi được trong khoảng thời gian \[7\] giây cuối \[\left( {8 \le t \le 15} \right)\] là:

A. \(147\,\,m\).

B. \(93,5\,\,m\).

C. \[77\,\,m\].

D. \(73,5\,\,m\).

Lời giải

Gọi hàm vận tốc thời gian \(7\) giây cuối \[\left( {8 \le t \le 15} \right)\] có dạng là \[\left( d \right):{\rm{ }}v\left( t \right) = {\rm{ }}at + b\].

Đường thẳng \[\left( d \right)\] đi qua hai điểm \[\left( {8\,;21} \right)\] và \[\left( {15\,;0} \right)\] nên ta có hệ phương trình:

\(\left\{ \begin{array}{l}8a + b = 21\\15a + b = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - 3\\b = 45\end{array} \right.\)\[ \Rightarrow \left( d \right):v\left( t \right) = - 3t + 45\].

Quãng đường chất điểm đi được trong thời gian \[7\] giây cuối \[\left( {8 \le t \le 15} \right)\] là:

\(S = \int\limits_8^{15} {v\left( t \right)dt} = \int\limits_8^{15} {\left( { - 3t + 45} \right)\,dt = 73,5\,\,(m)} \). Chọn D.

Câu 3