Dựa vào thông tin dưới đây để trả lời các câu từ 85 đến 87
Trong không gian cho các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz vuông góc với nhau từng đôi một sao cho \(OA = a\,\left( {a > 0} \right),\,OB = a\sqrt 2 ,\,OC = c\left( {c > 0} \right)\). Gọi D là đỉnh đối diện với O của hình chữ nhật AOBD và M là trung điểm của đoạn BC. \(\left( P \right)\) là mặt phẳng đi qua AM và cắt mặt phẳng \(\left( {OCD} \right)\) theo một đường thẳng vuông góc với đường thẳng AM.
Gọi E là giao điểm của \(\left( P \right)\) với đường thẳng \(OC\), độ dài đoạn thẳng OE là:
Dựa vào thông tin dưới đây để trả lời các câu từ 85 đến 87
Trong không gian cho các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz vuông góc với nhau từng đôi một sao cho \(OA = a\,\left( {a > 0} \right),\,OB = a\sqrt 2 ,\,OC = c\left( {c > 0} \right)\). Gọi D là đỉnh đối diện với O của hình chữ nhật AOBD và M là trung điểm của đoạn BC. \(\left( P \right)\) là mặt phẳng đi qua AM và cắt mặt phẳng \(\left( {OCD} \right)\) theo một đường thẳng vuông góc với đường thẳng AM.
Câu hỏi trong đề: Đề thi ĐGNL ĐHQG Hồ Chí Minh (V-ACT) năm 2026-2027 (Đề 24) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
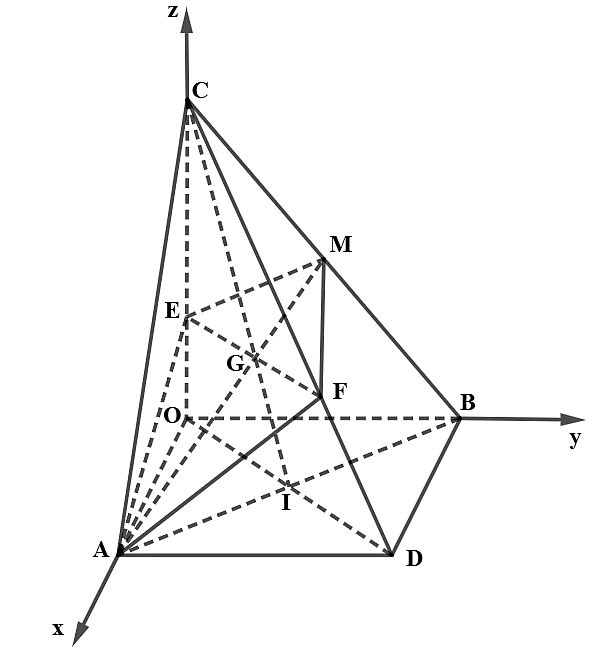
Cách 1: Giả sửa I là giao điểm của OD và AB, F là giao điểm của mặt phẳng \(\left( P \right)\) với CD. Khi đó dễ thấy ba đường thẳng EF, AM và CI đồng quy tại trọng tâm G của tam giác ABC.
Đặt \(\overrightarrow {OE} = k\overrightarrow {OC} \).
Từ giả thiết \(GA \bot GE\), ta có \(\overrightarrow {GA} \cdot \overrightarrow {GE} = 0\).
Mặt khác \(\overrightarrow {GA} \cdot \overrightarrow {GE} = \left( {\overrightarrow {OA} - \overrightarrow {OG} } \right) \cdot \left( {\overrightarrow {OE} - \overrightarrow {OG} } \right)\)
\( = \left[ {\overrightarrow {OA} - \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)} \right] \cdot \left[ {k\overrightarrow {OC} - \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)} \right]\)\( = - \frac{1}{3}{\overrightarrow {OA} ^2} + \frac{1}{9}{\overrightarrow {OA} ^2} + \frac{1}{9}{\overrightarrow {OB} ^2} + \frac{1}{9}{\overrightarrow {OC} ^2} - \frac{1}{3}k{\overrightarrow {OC} ^2}\) (vì \(\overrightarrow {OA} \cdot \overrightarrow {OB} = \overrightarrow {OB} \cdot \overrightarrow {OC} = \overrightarrow {OC} \cdot \overrightarrow {OA} = 0\))
\( = - \frac{1}{3}{a^2} + \frac{1}{9}{a^2} + \frac{2}{9}{a^2} + \frac{1}{9}{c^2} - \frac{k}{3}{c^2}\) (vì \(OA = a,\,OB = a\sqrt 2 ,\,OC = c\)).
Vậy \(\overrightarrow {GA} \cdot \overrightarrow {GE} = 0 \Leftrightarrow \frac{1}{9}{c^2} - \frac{k}{3}{c^2} = 0 \Leftrightarrow k = \frac{1}{3}\). Vậy \(OE = \frac{c}{3}\).
Cách 2: Chọn hệ tọa độ Oxyz như hình vẽ thì \(A\left( {a\,;\,0\,;\,0} \right),\,B\left( {0\,;\,a\sqrt 2 \,;\,0} \right),\,D\left( {a\,;\,a\sqrt 2 \,;\,0} \right),\,C\left( {0\,;\,0\,;\,c} \right)\), \(M\left( {0\,;\,\frac{{a\sqrt 2 }}{2}\,;\,\frac{c}{2}} \right)\). Ta lập được phương trình mặt phẳng \(\left( P \right)\) là: \(c\sqrt 2 \left( {x - a} \right) - cy + 3a\sqrt 2 z = 0\).
Giao điểm của \(\left( P \right)\) với trục Oz là \(E\left( {0\,;\,0\,;\,\frac{c}{3}} \right)\). Suy ra \(OE = \frac{c}{3}\). Chọn B.
Câu hỏi cùng đoạn
Câu 2:
Tỉ số thể tích của hai khối đa diện được tạo thành khi cắt khối chóp \(C.AOBD\) bởi mặt phẳng \(\left( P \right)\) là:
Giải bởi Vietjack
Vì \(\overrightarrow {OE} = \frac{1}{3}\overrightarrow {OC} \), giao tuyến EF của \(\left( P \right)\) với \(\left( {OCD} \right)\) song song với OD nên \(\overrightarrow {DF} = \frac{1}{3}\overrightarrow {DC} \).
Ta có \(\frac{{{V_{C.AEF}}}}{{{V_{C.AOD}}}} = \frac{{CE}}{{CO}} \cdot \frac{{CF}}{{CD}} = \frac{2}{3} \cdot \frac{2}{3} = \frac{4}{9}\), \(\frac{{{V_{C.MEF}}}}{{{V_{C.BOD}}}} = \frac{{CM}}{{CB}} \cdot \frac{{CE}}{{CO}} \cdot \frac{{CF}}{{CD}} = \frac{1}{2} \cdot \frac{2}{3} \cdot \frac{2}{3} = \frac{2}{9}\).
Vậy \({V_{C.AEMF}} = \left( {\frac{4}{9} + \frac{2}{9}} \right)\frac{1}{2}{V_{C.AOBD}} = \frac{1}{3}{V_{C.AOBD}}\), từ đó \(\frac{{{V_{C.AEMF}}}}{{{V_{AEMFDBO}}}} = \frac{1}{2}\). Chọn D.
Câu 3:
Khoảng cách từ điểm C đến mặt phẳng \(\left( P \right)\) là:
Giải bởi Vietjack
Cách 1: Tứ giác lồi AEMF có các đường chéo AM, EF vuông góc với nhau nên có diện tích \({S_{AEMF}} = \frac{1}{2}AM \cdot EF = \frac{1}{2}\sqrt {A{O^2} + O{J^2} + J{M^2}} \cdot \frac{2}{3}OD\) (J là trung điểm của OB)
\( = \frac{1}{2}\sqrt {{a^2} + \frac{{{a^2}}}{2} + \frac{{{c^2}}}{4}} \cdot \frac{2}{3}\sqrt {{a^2} + 2{a^2}} = \frac{{\sqrt 3 }}{6}a\sqrt {6{a^2} + {c^2}} \).
Vậy khoảng cách điểm C đến mặt phẳng \(\left( P \right)\) là:
\(d\left( {C,\,\left( P \right)} \right) = \frac{{3{V_{C.AEMF}}}}{{{S_{AEMF}}}} = \frac{{{a^2}c\frac{{\sqrt 2 }}{3}}}{{\frac{{\sqrt 3 }}{6}a\sqrt {6{a^2} + {c^2}} }} = \frac{{2ac\sqrt 6 }}{{3\sqrt {6{a^2} + {c^2}} }}\).
Cách 2: Sử dụng công thức tính khoảng cách trong không gian Oxyz, ta tính được khoảng cách từ điểm \(C\left( {0\,;\,0\,;\,c} \right)\) đến mặt phẳng \(\left( P \right)\) có phương trình \(c\sqrt 2 \left( {x - a} \right) - cy + 3a\sqrt 2 z = 0\) là:
\(d\left( {C,\,\left( P \right)} \right) = \frac{{\left| { - ac\sqrt 2 + 3ac\sqrt 2 } \right|}}{{\sqrt {2{c^2} + {c^2} + 18{a^2}} }} = \frac{{2ac\sqrt 6 }}{{3\sqrt {{c^2} + 6{a^2}} }}\). Chọn C.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Xét các biến cố:
\(M\): “Công ty \(X\) thuê công ty vệ tinh \(A\) tư vấn”;
\(N\): “Công ty \(X\) có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn”.
Ta có \(0,4 + 0,6 = 1\), do đó \(\overline M \) là biến cố: “Công ty \(X\) thuê công ty vệ tinh \(B\) tư vấn”.
Theo bài ra, ta có: \(P\left( M \right) = 0,4\); \[P\left( {\overline M } \right) = 0,6\]; \(P\left( {N|M} \right) = 0,05\); \(P\left( {N|\overline M } \right) = 0,03\).
Áp dụng công thức xác suất toàn phần, ta có:
\(P\left( N \right) = P\left( M \right) \cdot P\left( {N|M} \right) + P\left( {\overline M } \right) \cdot P\left( {N|\overline M } \right) = 0,4 \cdot 0,05 + 0,6 \cdot 0,03 = 0,038\).
Vậy xác suất để \(X\) có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn là \(0,038\). Chọn A.
Câu 2
Lời giải
Ta có \(d\left( {A,\left( P \right)} \right) = \frac{{\left| {1 + 4 + 4} \right|}}{{\sqrt {{1^2} + {1^2} + {1^2}} }} = 3\sqrt 3 .\) Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập