(1,5 điểm). Cho góc bẹt \(\widehat {xOy}\). Vẽ tia \(Oz\) sao cho \(\widehat {xOz} = 70^\circ \).
a) Tính \(\widehat {zOy}\).
(1,5 điểm). Cho góc bẹt \(\widehat {xOy}\). Vẽ tia \(Oz\) sao cho \(\widehat {xOz} = 70^\circ \).
a) Tính \(\widehat {zOy}\).
Câu hỏi trong đề: Bộ 3 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
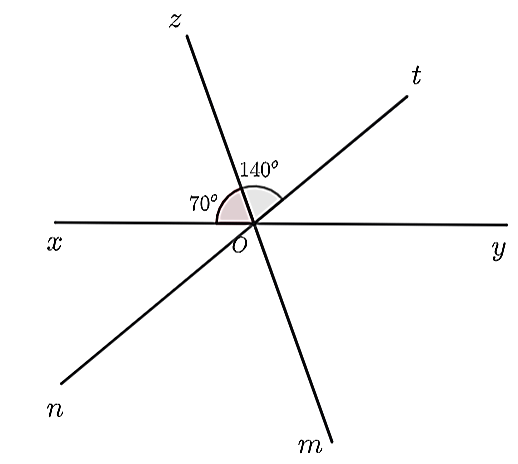
a) Ta có \(\widehat {xOz}\) và \(\widehat {zOy}\) là hai góc kề nhau nên \(\widehat {xOz} + \widehat {zOy} = \widehat {xOy}\), mà \(\widehat {xOy}\) là góc bẹt nên \(\widehat {xOy} = 180^\circ \)
Do đó, \(\widehat {xOz} + \widehat {zOy} = 180^\circ \), suy ra \(\widehat {zOy} = 180^\circ - \widehat {xOz} = 180^\circ - 70^\circ = 110^\circ \).
Vậy \(\widehat {zOy} = 110^\circ \).
Câu hỏi cùng đoạn
Câu 2:
b) Trên nửa mặt phẳng bờ \(Ox\) chứa \(Oz\), vẽ tia \(Ot\) sao cho \(\widehat {xOt} = 140^\circ \). Chứng minh \(Oz\) là tia phân giác của \(\widehat {xOt}\).
b) Trên nửa mặt phẳng bờ \(Ox\) chứa \(Oz\), vẽ tia \(Ot\) sao cho \(\widehat {xOt} = 140^\circ \). Chứng minh \(Oz\) là tia phân giác của \(\widehat {xOt}\).
b) Ta có: \(\widehat {xOt} > \widehat {xOz}{\rm{ }}\left( {140^\circ > 70^\circ } \right)\) nên tia \(Oz\) nằm giữa hai tia \(Ox,Ot.\)
Ta có: \(\widehat {xOt} + \widehat {zOt} = \widehat {xOz}{\rm{ }}\)hay \(\widehat {tOz} = \widehat {xOt} - \widehat {xOz{\rm{ }}} = 140^\circ - 70^\circ = 70^\circ \).
Suy ra \(\widehat {xOz} = \widehat {zOt} = 70^\circ \) và tia \(Oz\) nằm giữa hai tia \(Ox,Ot.\)
Do đó, \(Oz\) là tia phân giác của \(\widehat {xOt}\).
Câu 3:
c) Vẽ tia \(Om\) là tia đối của tia \(Oz\), tia \(On\) là tia đối của tia \(Ot\). Tính \(\widehat {yOm}\) và so sánh với \(\widehat {xOn}\).
c) Vẽ tia \(Om\) là tia đối của tia \(Oz\), tia \(On\) là tia đối của tia \(Ot\). Tính \(\widehat {yOm}\) và so sánh với \(\widehat {xOn}\).
c) Do tia \(Om\) là tia đối của tia \(Oz\) nên \(\widehat {zOx} = \widehat {yOm} = 70^\circ \) (hai góc đối đỉnh).
Ta có: tia \(On\) là tia đối của tia \(Ot\) nên \(\widehat {nOt} = 180^\circ \).
Có \(\widehat {xOn} + \widehat {xOt} = \widehat {nOt}\) (hai góc kề bù) nên \(\widehat {nOx} = 180^\circ - \widehat {xOt} = 180^\circ - 140^\circ = 40^\circ \).
Suy ra \(\widehat {nOx} < \widehat {yOm}{\rm{ }}\left( {40^\circ < 70^\circ } \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án: \( - 0,6\)
Ta có: \(\frac{2}{3}x + \frac{7}{{10}} = \frac{3}{{10}}\)
\(\frac{2}{3}x = \frac{3}{{10}} - \frac{7}{{10}}\)
\(\frac{2}{3}x = - \frac{2}{5}\)
\(x = - \frac{2}{5}:\frac{2}{3}\)
\(x = - \frac{2}{5}.\frac{3}{2}\)
\(x = - \frac{3}{5}\) hay \(x = - 0,6.\)
Vậy \(x = - 0,6.\)
Lời giải
Hướng dẫn giải
a) \(\frac{{13}}{{25}} - \frac{{11}}{4} - \frac{{38}}{{25}} + \frac{{15}}{4} + \frac{1}{2} = \left( {\frac{{13}}{{25}} - \frac{{28}}{{25}}} \right) + \left( {\frac{{15}}{4} - \frac{{11}}{4}} \right) + \frac{1}{2} = \frac{{ - 15}}{{25}} + 1 + \frac{1}{2} = \frac{{ - 3}}{5} + 1 + \frac{1}{2} = \frac{2}{5} + \frac{1}{2} = \frac{9}{{10}}\).
b) \({\left( {\frac{1}{2} - \frac{2}{3}} \right)^2} + 1\frac{2}{3}:\left| { - 0,75} \right| - \sqrt {\frac{1}{{16}}} = {\left( { - \frac{1}{6}} \right)^2} + \frac{5}{3}:0,75 - \frac{1}{4}\)
\( = \frac{1}{{36}} + \frac{5}{3}.\frac{4}{3} - \frac{1}{4}\)
\( = \frac{1}{{36}} + \frac{{20}}{9} - \frac{1}{4}\)
\( = \frac{1}{{36}} + \frac{{80}}{{36}} - \frac{9}{{36}} = \frac{{72}}{{36}} = 2\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.