Câu hỏi:
06/06/2025 21
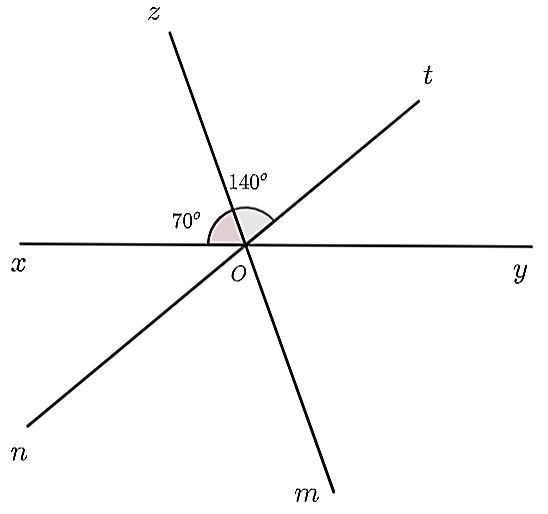
Cho góc bẹt \(\widehat {xOy}\). Vẽ tia \(Oz\) sao cho \(\widehat {xOz} = 70^\circ \). Trên nửa mặt phẳng bờ \(Ox\) chứa tia \(Oz\) vẽ tia \(Ot\) sao cho \(\widehat {xOt} = 140^\circ .\)Vẽ tia \(Om\) là tia đối của tia \(Oz\), tia \(On\) là tia đối của tia \(Ot.\)
a) \(\widehat {mOy} = 70^\circ \).
b) \(\widehat {xOt}\) và \(\widehat {xOn}\) là hai góc kề bù.
c) \(\widehat {zOy} = 140^\circ \).
d) \(Om\) là tia phân giác của \(\widehat {nOy}.\)
Cho góc bẹt \(\widehat {xOy}\). Vẽ tia \(Oz\) sao cho \(\widehat {xOz} = 70^\circ \). Trên nửa mặt phẳng bờ \(Ox\) chứa tia \(Oz\) vẽ tia \(Ot\) sao cho \(\widehat {xOt} = 140^\circ .\)Vẽ tia \(Om\) là tia đối của tia \(Oz\), tia \(On\) là tia đối của tia \(Ot.\)
a) \(\widehat {mOy} = 70^\circ \).
b) \(\widehat {xOt}\) và \(\widehat {xOn}\) là hai góc kề bù.
c) \(\widehat {zOy} = 140^\circ \).
d) \(Om\) là tia phân giác của \(\widehat {nOy}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: a) Đ b) S c) S d) Đ
a) Ta có: \(\widehat {xOz} = \widehat {mOy} = 70^\circ \) (đối đỉnh). Do đó, ý a) đúng.
b) Ta có tia \(On\) là tia đối của tia \(Ot\) nên \(\widehat {xOt}\) và \(\widehat {xOn}\) là hai góc kề bù. Do đó, ý b) đúng.
c) Có \(\widehat {xOz}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOz} + \widehat {zOy} = 180^\circ \).
Suy ra \(\widehat {yOz} = 180^\circ - \widehat {xOz} = 180^\circ - 70^\circ = 110^\circ \).
Do đó, ý c) sai.
d) Ta có: \(\widehat {xOz} = \widehat {mOy} = 70^\circ \) (đối đỉnh); \(\widehat {xOt} = \widehat {nOy} = 140^\circ \) (đối đỉnh)
Nhận thấy \(\widehat {mOy} < \widehat {nOy}{\rm{ }}\left( {70^\circ < 140^\circ } \right)\) nên \(Om\) nằm giữa hai tia \(On,Oy\).
Có \(\widehat {mOy} = \frac{1}{2}\widehat {nOy}\) nên \(Om\) là tia phân giác của \(\widehat {nOy}.\)
Vậy ý d) là đúng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 8 (chương trình mới) ( 120.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án: \(1\)
Ta có: \({\left( {x - 3} \right)^3} + \frac{{41}}{5} = \frac{1}{5}\)
\({\left( {x - 3} \right)^3} = \frac{1}{5} - \frac{{41}}{5}\)
\({\left( {x - 3} \right)^3} = - 8\)
\({\left( {x - 3} \right)^3} = {\left( { - 2} \right)^3}\)
\(x - 3 = - 2\)
\(x = - 2 + 3\)
\(x = 1\).
Vậy \(x = 1\).
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có: \(0,15 = \frac{{15}}{{100}} = \frac{3}{{20}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
Đề thi giữa học kì 2 Toán 7 KNTT - Đề 01 có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận