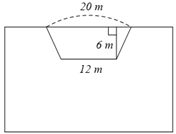
Khẳng định nào dưới đây là sai?
Câu hỏi trong đề: Đề kiểm tra giữa kì 1 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
Khẳng định “Tổng của hai hợp số luôn là một hợp số” là sai. Chẳng hạn trong trường hợp có hai số 9 và 14 đều là hợp số, nhưng tổng của hai số này là \(9 + 14 = 23\) lại là một số nguyên tố.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) \[\left( {{3^5} \cdot {3^7}} \right):{3^{10}} + 5 \cdot {2^4} - {7^3}:7\] \[ = {3^{12}}:{3^{10}} + 5 \cdot 16 - {7^2}\] \[ = {3^2} + 80 - 49\] \( = 9 + 80 - 49\) \( = 40\). |
b) \[1\,\,754:17 - 74:17 + 20:17\] \[ = \left( {1\,\,754 - 74 + 20} \right):17\] \[ = 1\,\,700:17\] \[ = 100.\] |
Lời giải
Hướng dẫn giải
Đáp số: 2.
Ta có:
\({2^{x + 2}} \cdot {3^{x + 1}} \cdot {5^x} = 10\,\,800\)
\({2^{x + 2}} \cdot {3^{x + 1}} \cdot {5^x} = {2^4} \cdot {3^3} \cdot {5^2}\)
Suy ra \(x + 2 = 4;\,\,x + 1 = 3\) và \(x = 2.\)
Do đó \(x = 2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.