Cho \(B - \left( {5{x^2} - 2xyz} \right) = 2{x^2} + 2xyz + 1\). Hạng tử tự do của đa thức \(B\) là bao nhiêu?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp số: 1.
Ta có \(B - \left( {5{x^2} - 2xyz} \right) = 2{x^2} + 2xyz + 1\)
Suy ra \[B = \left( {2{x^2} + 2xyz + 1} \right) + \left( {5{x^2} - 2xyz} \right)\]
\( = 2{x^2} + 2xyz + 1 + 5{x^2} - 2xyz\)
\( = \left( {2{x^2} + 5{x^2}} \right) + \left( {2xyz - 2xyz} \right) + 1 = 7{x^2} + 1\).
Do đó, hạng tử tự do của đa thức \(B\) là 1.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
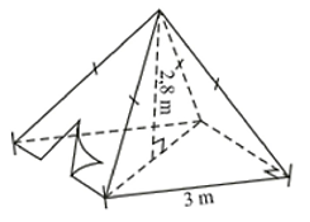
a) Diện tích đáy hình vuông của chiếc lều là:
Thể tích không khí bên trong chiếc lều là:
Chú ý: Có thể không cần bước tính diện tích đáy.
b) Diện tích xung quanh của chiếc lều là:
\({S_{xq}} = \frac{1}{2} \cdot C \cdot d = \frac{1}{2} \cdot \left( {4 \cdot 3} \right) \cdot 3,18 = 19,08\;\;\left( {{{\rm{m}}^2}} \right)\)
Diện tích vải phủ bốn phía và trải nền đất cho chiếc lều là:
\(S = 9 + 19,08 = 28,08\) (m2).
Do \(28,08 > 20\) nên số tiền mua vải được giảm giá \(5\% \) trên tổng hóa đơn.
Vậy số tiền mua vải là: \(28,08 \cdot 15\,\,000 \cdot \left( {100\% - 5\% } \right) = 400\,\,140\) (đồng).
Lời giải
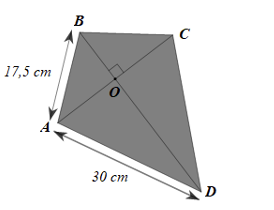
a) Số đo góc \(D\) ở đuôi chiếc diều là:
\(\widehat D = 360^\circ - \left( {\widehat {A\,\,} + \widehat {B\,} + \widehat {C\,}} \right) = 360^\circ - \left( {102^\circ + 102^\circ + 102^\circ } \right) = 54^\circ .\)
b) Xét \(\Delta OAD\) vuông tại \(O\), theo định lí Pythagore ta có:
\(O{A^2} = A{D^2} - O{D^2} = {30^2} - {26,7^2} = 187,11\)
Xét \(\Delta OAB\) vuông tại \(O,\) theo định lí Pythagore ta có:
\(O{B^2} = A{B^2} - O{A^2} = {17,5^2} - 187,11 = 119,14\)
Do đó \(OB = \sqrt {119,14} \approx 10,9\) (cm).
Suy ra \(BD = OB + OD \approx 10,9 + 26,7 = 37,6\) (cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.