(0,5 điểm) Rút gọn biểu thức: \[A = \frac{1}{3} + \frac{2}{{{3^2}}} + \frac{3}{{{3^3}}} + ... + \frac{{99}}{{{3^{99}}}} + \frac{{100}}{{{3^{100}}}}.\]
Quảng cáo
Trả lời:
Hướng dẫn giải
Ta có: \[3A = 1 + \frac{2}{3} + \frac{3}{{{3^2}}} + ... + \frac{{99}}{{{3^{98}}}} + \frac{{100}}{{{3^{99}}}}\]
Suy ra \[3A - A = \left( {1 + \frac{2}{3} + \frac{3}{{{3^2}}} + ... + \frac{{99}}{{{3^{98}}}} + \frac{{100}}{{{3^{99}}}}} \right) - \left( {\frac{1}{3} + \frac{2}{{{3^2}}} + \frac{3}{{{3^3}}} + ... + \frac{{99}}{{{3^{99}}}} + \frac{{100}}{{{3^{100}}}}} \right)\]
\[2A = 1 + \frac{1}{3} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{3^{98}}}} + \frac{1}{{{3^{99}}}} - \frac{{100}}{{{3^{100}}}}\]
Đặt \[B = 1 + \frac{1}{3} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{3^{98}}}} + \frac{1}{{{3^{99}}}}\].
Ta có \[3B = 3 + 1 + \frac{1}{3} + ... + \frac{1}{{{3^{97}}}} + \frac{1}{{{3^{98}}}}\]
Suy ra \[3B - B = \left( {3 + 1 + \frac{1}{3} + ... + \frac{1}{{{3^{97}}}} + \frac{1}{{{3^{98}}}}} \right) - \left( {1 + \frac{1}{3} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{3^{98}}}} + \frac{1}{{{3^{99}}}}} \right)\]
\[2B = 3 - \frac{1}{{{3^{99}}}}\]
\[B = \frac{3}{2} - \frac{1}{{{3^{99}} \cdot 2}}\]
Do đó \[2A = \frac{3}{2} - \frac{1}{{{3^{99}} \cdot 2}} - \frac{{100}}{{{3^{100}}}}\]
Khi đó, \[A = \frac{3}{4} - \frac{1}{{{3^{99}} \cdot 4}} - \frac{{100}}{{{3^{100}} \cdot 2}} = \frac{{3 \cdot {3^{100}} - 3 - 2 \cdot 100}}{{4 \cdot {3^{100}}}} = \frac{{3 \cdot {3^{100}} - 203}}{{4 \cdot {3^{100}}}}.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Diện tích xung quanh của bể nước là: \(2.\left( {10 + 3} \right).1,25 = 32,5\) (m2).
Diện tích đáy của bể nước là: \(3.10 = 30\) (m2).
Do đó, diện tích phần bể cần lát gạch là: \(32,5 + 30 = 62,5\) (m2).
Diện tích một viên gạch men là: \(50.50 = 2{\rm{ }}500\) (cm2) \( = 0,25{\rm{ }}{{\rm{m}}^2}\).
Do đó, số viên gạch men cần để lát bể nước đó là: \(62,5:0,25 = 250\) (viên).
Số tiền để mua gạch men để lát kín đáy và xung quanh bể nước đó là:
\(17{\rm{ }}000.250 = 4{\rm{ }}250{\rm{ }}000\) (đồng).
Câu 2
A. \(\mathbb{N}.\)
B. \(\mathbb{Z}.\)
C. 𝕀.
D. \(\mathbb{Q}.\)
Lời giải
Đáp án đúng là: C
Ta có tập hợp các số vô tỉ được kí hiệu là 𝕀.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
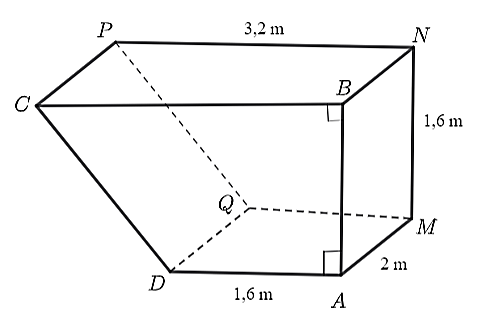
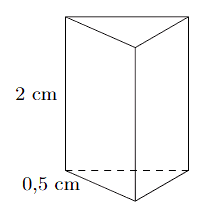
A. Các mặt đáy song song với nhau.
B. Các mặt đáy đều là hình tam giác.
C. Các mặt bên đều là hình chữ nhật.
D. Các mặt đáy đều là hình tứ giác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.