Câu hỏi:
29/06/2025 12(3,0 điểm)
1. a) Hãy vẽ để tìm tâm đối xứng và trục đối xứng (nếu có) của hình chữ nhật dưới đây:
b)
Trong hình dưới đây, bông hoa nào là hình có trục đối xứng, bông hoa nào là hình có tâm đối xứng?
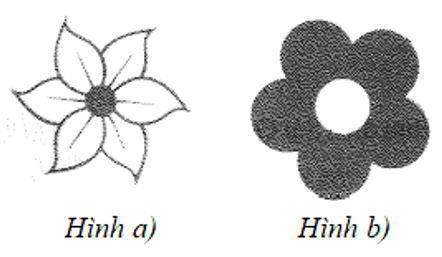
2. Trên mảnh đất hình chữ nhật có chiều dài \(8\,\,{\rm{m,}}\) chiều rộng \(6\,\,{\rm{m}}\), người ta chia phân khu vực để trồng hoa, trồng cỏ như hình bên. Hoa sẽ được trồng ở khu vực hình bình hành \[EFKD\] và \[GBHI,\] cỏ sẽ được trồng ở các phần đất còn lại.
b) Tính diện tích trồng hoa.
c) Tiền công để trả cho mỗi mét vuông trồng hoa là \(80\,\,000\) đồng và cho mỗi mét vuông trồng cỏ là \(60\,\,000\) đồng. Tính số tiền công cần chi trả để trồng hoa và cỏ.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
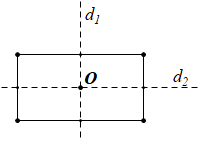
1. a) Tâm đối xứng \(O\) và các trục đối xứng \({d_1},{d_2}\) của hình chữ nhật đã cho được vẽ như hình dưới đây:
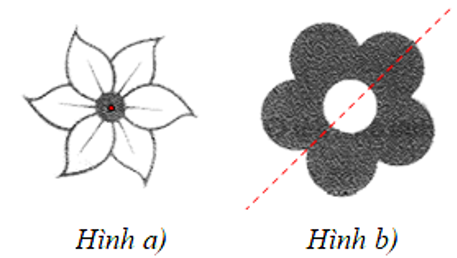
b) Bông hoa ở Hình a) có tâm đối xứng và bông hoa ở Hình b) có trục đối xứng:
2. a) Hai hình bình hành \[EFKD\] và \[GBHI\] có kích thước bằng nhau nên diện tích hình bình hành \[EFKD\] và diện tích hình bình hành \[GBHI\] bằng nhau.
Diện tích trồng hoa là: \[2 \cdot \left( {1,8 \cdot 6} \right) = 21,6{\rm{\;}}\,\left( {{{\rm{m}}^2}} \right){\rm{.}}\]
Vậy diện tích trồng hoa là \[21,6{\rm{\;}}{{\rm{m}}^2}{\rm{.}}\]
b) Diện tích mảnh đất là: \(8 \cdot 6 = 48{\rm{\;}}\,\left( {{{\rm{m}}^2}} \right){\rm{.}}\)
Diện tích trồng cỏ là: \(48 - 21,6 = 26,4{\rm{\;\;}}\,\left( {{{\rm{m}}^2}} \right){\rm{.}}\)
Tiền công trả cho trồng hoa là:
\(80\,\,000 \cdot 21,6 = 1\,\,728\,\,000\) (đồng).
Tiền công trả cho trồng cỏ là:
\(60\,\,000 \cdot 26,4 = 1\,\,584\,\,000\) (đồng).
Tiền công cần chi trả cho trồng cả hoa và cỏ là:
\(1\,\,728\,\,000 + 1\,\,584\,\,000 = 3\,\,312\,\,000\) (đồng).
Vậy số tiền công cần chi trả để trồng hoa và cỏ là \(3\,\,312\,\,000\) đồng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
|
a) \(15x + 25 = 100\) \(15x = 75\) \(x = 5\) Vậy \(x = 5\). |
b) \(3 - \left( {x - 17} \right) = 289 - \left( {36 + 289} \right)\) \(3 - \left( {x - 17} \right) = 289 - 36 - 289\) \(3 - \left( {x - 17} \right) = - 36\) \(x - 17 = 3 - \left( { - 36} \right)\) \(x - 17 = 39\) \(x = 56\) Vậy \(x = 56\). |
c) \({2^{x + 3}}{.2^2} = {2^2}.3 + 52\) \({2^{x + 5}} = 4.3 + 52\) \({2^{x + 5}} = 64 = {2^6}\) Suy ra \(x + 5 = 6\) \(x = 1\) Vậy \(x = 1\). |
Lời giải
Hướng dẫn giải
|
a) \(4 \cdot {5^2} - 18:{3^2}\) \( = 4 \cdot 25 - 18:9\) \( = 100 - 2\) \( = 98\). c) \[25 \cdot 75 - 3 \cdot 70 + 25 \cdot 125 - 3 \cdot 130\] \[ = \left( {25 \cdot 75 + 25 \cdot 125} \right) - \left( {3 \cdot 70 + 3 \cdot 130} \right)\] \[ = 25 \cdot \left( {75 + 125} \right) - 3 \cdot \left( {70 + 130} \right)\] \[ = 25 \cdot 200 - 3 \cdot 200\] \[ = 200 \cdot \left( {25 - 3} \right)\] \[ = 200 \cdot 22\] \[ = 4\,\,400\]. |
b) \[\left( {1\,\,267 - 196} \right) - \left( {267 + 304} \right)\] \[ = 1\,\,267 - 196 - 267 - 304\] \[ = \left( {1\,\,267 - 267} \right) - \left( {196 + 304} \right)\] \[ = 1\,\,000 - 500\] \[ = 500\]. d) \[\left( { - 16} \right) \cdot 125 \cdot \left[ {\left( { - 5} \right) \cdot {2^2}} \right] \cdot {5^4} - 12 \cdot {10^6}\] \( = \left( { - {2^4}} \right) \cdot {5^3} \cdot \left[ {\left( { - 5} \right) \cdot {2^2}} \right] \cdot {5^4} - 12 \cdot {10^6}\) \( = \left( { - {2^4} \cdot {2^2}} \right) \cdot \left[ {{5^3} \cdot \left( { - 5} \right) \cdot {5^4}} \right] - 12 \cdot {10^6}\) \( = \left( { - {2^6}} \right) \cdot \left( { - {5^8}} \right) - 12 \cdot {10^6}\) \( = {2^6} \cdot {5^8} - 12 \cdot {10^6}\) \( = {2^6} \cdot {5^6} \cdot {5^2} - 12 \cdot {10^6}\) \( = {10^6} \cdot 25 - 12 \cdot {10^6}\) \[ = {10^6} \cdot \left( {25 - 12} \right)\] \( = {10^6} \cdot 13\) \( = 13\,\,000\,\,000\). |
\ [= \ left ({25 \ cdot 75 + 25 \ cdot 125} \ right) - \ left ({3 \ cdot 70 + 3 \ cdot 130} \ right) \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
(0,5 điểm) Một hiệu sách có năm hộp bút bi và bút chì. Mỗi hộp chỉ đựng một loại bút.
|
Hộp 1 |
Hộp 2 |
Hộp 3 |
Hộp 4 |
Hộp 5 |
|
78 chiếc |
80 chiếc |
82 chiếc |
114 chiếc |
128 chiếc |
Sau khi bán một hộp bút chì thì số bút bi còn lại gấp bốn lần số bút chì còn lại. Hãy cho biết lúc đầu hộp nào đựng bút bi, hộp nào đựng bút chì?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo