3.1. Tung \(30\) lần hai đồng xu cân đối và đồng chất ta được kết quả như sau:
Mặt
SN
SS
NN
Số lần xuất hiện
18
8
4
Tính xác suất thực nghiệm của sự kiện “Xuất hiện ít nhất một mặt sấp”
3.2. Chứng tỏ rằng \(\frac{1}{{11}} + \frac{1}{{12}} + \frac{1}{{13}} + ... + \frac{1}{{70}} < \frac{5}{2}.\)
3.1. Tung \(30\) lần hai đồng xu cân đối và đồng chất ta được kết quả như sau:
|
Mặt |
SN |
SS |
NN |
|
Số lần xuất hiện |
18 |
8 |
4 |
Tính xác suất thực nghiệm của sự kiện “Xuất hiện ít nhất một mặt sấp”
3.2. Chứng tỏ rằng \(\frac{1}{{11}} + \frac{1}{{12}} + \frac{1}{{13}} + ... + \frac{1}{{70}} < \frac{5}{2}.\)
Quảng cáo
Trả lời:
3.1. Số lần tung đồng xu là \(n = 30.\)
Để xuất hiện ít nhất một mặt sấp thì có thể xảy ra là mặt SN và SS.
Do đó, số lần tung được ít nhất một mặt sấp là: \(k = 18 + 8 = 26\).
Xác suất thực nghiệm của sự kiện “Xuất hiện ít nhất một mặt sấp” là: \(\frac{k}{n} = \frac{{26}}{{30}} = \frac{{13}}{{15}}.\)
3.2. Đặt \(A = \frac{1}{{11}} + \frac{1}{{12}} + \frac{1}{{13}} + ... + \frac{1}{{70}}\)
\(A = \frac{1}{{11}} + \frac{1}{{12}} + ... + \frac{1}{{20}} + \frac{1}{{21}} + ... + \frac{1}{{30}} + \frac{1}{{31}} + ... + \frac{1}{{40}} + \frac{1}{{41}} + ... + \frac{1}{{50}} + \frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}} + \frac{1}{{61}} + ... + \frac{1}{{70}}\)
\(A = \left( {\frac{1}{{11}} + ... + \frac{1}{{20}}} \right) + \left( {\frac{1}{{21}} + ... + \frac{1}{{30}}} \right) + \left( {\frac{1}{{31}} + ... + \frac{1}{{40}}} \right) + \left( {\frac{1}{{41}} + ... + \frac{1}{{50}}} \right) + \left( {\frac{1}{{51}} + ... + \frac{1}{{60}}} \right) + \left( {\frac{1}{{61}} + ... + \frac{1}{{70}}} \right)\)
Nhận thấy \(\frac{1}{{11}} + \frac{1}{{12}} + ... + \frac{1}{{20}} < \frac{1}{{10}} + \frac{1}{{10}} + ... + \frac{1}{{10}}\) hay \(\frac{1}{{11}} + \frac{1}{{12}} + ... + \frac{1}{{20}} < \frac{1}{{10}}.10 = 1\).
\(\frac{1}{{21}} + \frac{1}{{22}} + ... + \frac{1}{{30}} < \frac{1}{{20}} + \frac{1}{{20}} + ... + \frac{1}{{20}}\) hay \(\frac{1}{{21}} + \frac{1}{{22}} + ... + \frac{1}{{30}} < \frac{1}{{20}}.10 = \frac{1}{2}\)
\(\frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{40}} < \frac{1}{{30}} + \frac{1}{{30}} + ... + \frac{1}{{30}}\) hay \(\frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{40}} < \frac{1}{{30}}.10 = \frac{1}{3}\)
\(\frac{1}{{41}} + \frac{1}{{42}} + ... + \frac{1}{{50}} < \frac{1}{{40}} + \frac{1}{{40}} + ... + \frac{1}{{40}}\) hay \(\frac{1}{{41}} + \frac{1}{{42}} + ... + \frac{1}{{50}} < \frac{1}{{40}}.10 = \frac{1}{4}\)
\(\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}} < \frac{1}{{50}} + \frac{1}{{50}} + ... + \frac{1}{{50}}\) hay \(\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}} < \frac{1}{{50}}.10 = \frac{1}{5}\)
\(\frac{1}{{61}} + \frac{1}{{62}} + ... + \frac{1}{{70}} < \frac{1}{{60}} + \frac{1}{{60}} + ... + \frac{1}{{60}}\) hay \(\frac{1}{{61}} + \frac{1}{{62}} + ... + \frac{1}{{70}} < \frac{1}{{60}}.10 = \frac{1}{6}\)
Do đó, \(A < 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6}\) hay \(A < \frac{{49}}{{20}} < \frac{{50}}{{20}} = \frac{5}{2}\).
Vậy \(\frac{1}{{11}} + \frac{1}{{12}} + \frac{1}{{13}} + ... + \frac{1}{{70}} < \frac{5}{2}\) (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
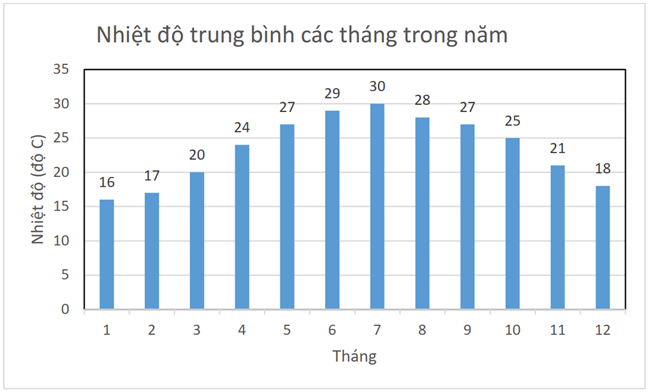
A. Tháng 5.
Lời giải
Đáp án đúng là: C
Tháng có nhiệt độ trung bình cao nhất là tháng 7 với nhiệt độ trung bình là \(30^\circ C\).
Lời giải
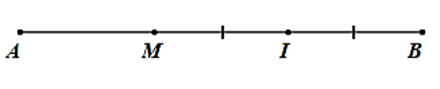
a) Trên \(AB\), có \(AM < AB{\rm{ }}\left( {3{\rm{ cm}} < 9{\rm{ cm}}} \right)\).
Nên \(M\) nằm giữa hai điểm \(A,B\).
Ta có: \(AM + MB = AB\) nên \(MB = AB - AM = 9 - 3 = 6{\rm{ cm}}{\rm{.}}\)
Mà \(I\) là trung điểm của \(MB\) nên \(MI = IB = \frac{1}{2}MB = 3{\rm{ cm}}{\rm{.}}\)
Vậy \(MI = 3{\rm{ cm}}{\rm{.}}\)
b) Vì \(M\) nằm giữa hai điểm \(A,B\) và \(I\) là trung điểm của \(MB\) nên \(M\) nằm giữa hai điểm \(A,I.\)
Mà \(MI = AM = 3{\rm{ cm}}{\rm{.}}\)
Do đó, \(M\) là trung điểm của đoạn thẳng \(AI.\)
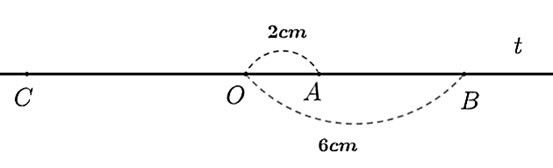
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. chia đoạn thẳng thành hai phần bằng nhau.
B. chia đoạn thẳng thành ba phần bằng nhau.
C. chia đoạn thẳng thành hai phần không bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.