Câu hỏi:
05/07/2025 20(2,0 điểm)
1. Giải các phương trình sau:
a) \[\left( {2x + 9} \right)\left( {\frac{2}{3}x - 5} \right) = 0\].
b) \(\frac{{2x + 1}}{{x + 1}} + \frac{2}{x} = \frac{2}{{x\left( {x + 1} \right)}}.\)
2. Giải các bất phương trình sau:
a) \[ - 4x + 3 \le 3x - 1.\]
b) \[\frac{{4x + 1}}{3} - \frac{{x - 5}}{4} \ge \frac{1}{2} - \frac{{3 - x}}{5}.\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
|
1. a) \[\left( {2x + 9} \right)\left( {\frac{2}{3}x - 5} \right) = 0\] \(2x + 9 = 0\) hoặc \[\frac{2}{3}x - 5 = 0\] \(2x = - 9\) hoặc \(\frac{2}{3}x = 5\) \(x = - \frac{9}{2}\) hoặc \(x = \frac{{15}}{2}\). Vậy phương trình đã cho có hai nghiệm là \(x = - \frac{9}{2};\,\,x = \frac{{15}}{2}\). |
1. b) Điều kiện xác định \(x \ne - 1,\,\,x \ne 0\). \(\frac{{2x + 1}}{{x + 1}} + \frac{2}{x} = \frac{2}{{x\left( {x + 1} \right)}}\) \(\frac{{\left( {2x + 1} \right)x}}{{x\left( {x + 1} \right)}} + \frac{{2\left( {x + 1} \right)}}{{x\left( {x + 1} \right)}} = \frac{2}{{x\left( {x + 1} \right)}}\) \(\left( {2x + 1} \right)x + 2\left( {x + 1} \right) = 2\) \(2{x^2} + x + 2x + 2 = 2\) \(2{x^2} + 3x = 0\) \(x\left( {2x + 3} \right) = 0\) \(x = 0\) hoặc \(2x + 3 = 0\) \(x = 0\) (không thỏa mãn) hoặc \(x = - \frac{3}{2}\) (thỏa mãn). Vậy nghiệm của phương trình đã cho là \(x = - \frac{3}{2}.\) |
|
2. a) \[ - 4x + 3 \le 3x - 1\] \[ - 4x - 3x \le - 1 - 3\] \[ - 7x \le - 4\] \[x \ge \frac{4}{7}.\] Vậy nghiệm của bất phương trình đã cho là \[x \ge \frac{4}{7}.\] |
2. b) \[\frac{{4x + 1}}{3} - \frac{{x - 5}}{4} \ge \frac{1}{2} - \frac{{3 - x}}{5}\] \[\frac{{20\left( {4x + 1} \right)}}{{60}} - \frac{{15\left( {x - 5} \right)}}{{60}} \ge \frac{{30 \cdot 1}}{{60}} - \frac{{12\left( {3 - x} \right)}}{{60}}\] \[20\left( {4x + 1} \right) - 15\left( {x - 5} \right) \ge 30 \cdot 1 - 12\left( {3 - x} \right)\] \[80x + 20 - 15x + 75 \ge 30 - 36 + 12x\] \[65x + 95 \ge - 6 + 12x\] \[53x \ge - 101\] \[x \ge - \frac{{101}}{{53}}\]. Vậy nghiệm của bất phương trình đã cho là \[x \ge - \frac{{101}}{{53}}\]. |
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Ta mô hình hóa bài toán như hình vẽ sau:
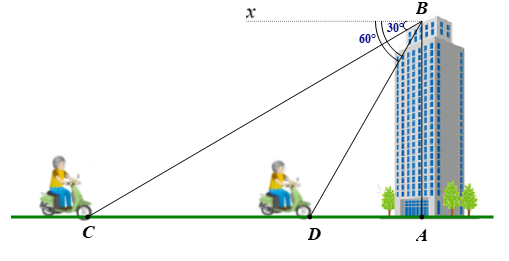
Do mặt đất là phương ngang nên \[\widehat {BCA} = \widehat {CBx} = 30^\circ \] và \[\widehat {BDA} = \widehat {ABx} - \widehat {DBx} = 90^\circ - 30^\circ = 60^\circ \].
Xét \[\Delta ABC\] vuông tại \[A\], ta có:
\[AC = AB \cdot \cot \widehat {BCA} = AB \cdot \cot 30^\circ = AB\sqrt 3 \].
Xét \[\Delta ABD\] vuông tại \[A\], ta có:
\[AD = AB \cdot \cot \widehat {BDA} = AB \cdot \cot 60^\circ = \frac{{AB\sqrt 3 }}{3}\].
Suy ra \[CD = AC - AD = AB\sqrt 3 - \frac{{AB\sqrt 3 }}{3} = AB\left( {\sqrt 3 - \frac{{\sqrt 3 }}{3}} \right) = AB \cdot \frac{{2\sqrt 3 }}{3} = \frac{{2AB\sqrt 3 }}{3} = 2AD\].
Như vậy, quãng đường \(CD\) gấp đôi quãng đường \(DA.\) Mà thời gian di chuyển tỉ lệ thuận với quãng đường đi được khi vận tốc không đổi nên thời gian xe máy di chuyển từ \(C\) đến \(D\) gấp đôi thời gian xe máy di chuyển từ \(D\) về \(A\).
Vậy thời gian để xe máy chạy từ \[D\] đến tòa nhà là \[\frac{6}{2} = 3\] (phút).
Lời giải
Hướng dẫn giải
1. Xét \(\Delta KEC\) vuông tại \(K\), ta có:
\(EK = EC \cdot \sin C = 16 \cdot \sin 30^\circ = 8{\rm{\;(cm)}}{\rm{.}}\)
Xét \(\Delta ABE\) vuông tại \(A\) có \(AE = AB\) nên \(\Delta ABE\) vuông cân tại \(A.\) Do đó \(\widehat {AEB} = 45^\circ .\)
Xét \(\Delta EBC\) có \(\widehat {EBK}\) là góc ngoài nên \(\widehat {EBK} = \widehat {AEB} + \widehat {C\,} = 45^\circ + 30^\circ = 75^\circ .\)
Xét \(\Delta KEB\) vuông tại \(K\) , ta có \(\sin \widehat {EBK} = \frac{{EK}}{{EB}}\).
Suy ra \(EB = \frac{{EK}}{{\sin \widehat {EBK}}} = \frac{8}{{\sin 75^\circ }} \approx 8,3{\rm{\;(cm)}}{\rm{.}}\)
Xét \(\Delta ABE\) vuông tại \(A\) ta có \(AB = EB \cdot \sin \widehat {AEB} \approx 8,3 \cdot \sin 45^\circ \approx 5,9{\rm{\;(cm)}}{\rm{.}}\)
|
2. Xét \(\Delta AEQ\) vuông tại \(A\) ta có: \(AQ = QE \cdot \sin \widehat {CEQ}.\) Xét \(\Delta ACQ\) vuông tại \(A\) ta có: \(AQ = CQ \cdot \sin \widehat {QCE}\). Suy ra \(QE \cdot \sin \widehat {CEQ} = CQ \cdot \sin \widehat {QCE}\) Do đó \[\frac{{QE}}{{\sin \widehat {QCE}}} = \frac{{CQ}}{{\sin \widehat {CEQ}}}.\] (1) Chứng minh tương tự ta có: \(CK = CQ \cdot \sin \widehat {EQC} = EC \cdot \sin \widehat {CEQ}\) Suy ra \[\frac{{EC}}{{\sin \widehat {EQC}}} = \frac{{CQ}}{{\sin \widehat {CEQ}}}.\] (2) Từ (1) và (2) ta có \[\frac{{QE}}{{\sin \widehat {QCE}}} = \frac{{EC}}{{\sin \widehat {EQC}}} = \frac{{CQ}}{{\sin \widehat {CEQ}}}.\] |
|
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo