Trong hai giá trị \(x = 1\) và \(x = 2\), giá trị nào là nghiệm của bất phương trình \(3x - 4 \le 0?\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp số: \(x = 1.\)
Thay \(x = 1\) vào bất phương trình, ta được \(3 \cdot 1 - 4 = - 1 \le 0\) là khẳng định đúng.
Do đó, \(x = 1\) là một nghiệm của bất phương trình đã cho.
Thay \(x = 2\) vào bất phương trình, ta được \(3 \cdot 2 - 4 = 2 \le 0\) là khẳng định sai.
Do đó, \(x = 2\) không là một nghiệm của bất phương trình đã cho.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
|
a) Xét \[\Delta ABH\] vuông tại \[H,\] ta có: \[AH = AB \cdot \sin B = 4 \cdot \sin 40^\circ \approx 2,57\] (cm); \(BH = AB \cdot \cos B = 4 \cdot \cos 40^\circ \approx 3,06\) (cm). Ta có \(BC = BH + HC\) Suy ra \(HC = BC - BH \approx 4,5 - 3,06 = 1,44\) (cm). |
|
Xét \[\Delta AHC\] vuông tại \[H\], theo định lí Pythagore, ta có:
\[A{C^2} = A{H^2} + H{C^2} \approx 2,{57^2} + 1,{44^2} = 8,6785\]
Suy ra \(AC \approx 2,95\) (cm).
Trong \[\Delta AHC\], ta cũng có: \(\tan C = \frac{{AH}}{{HC}} \approx \frac{{2,57}}{{1,44}} = \frac{{257}}{{144}}.\) Suy ra \(\widehat {C\,} \approx 60^\circ 44'.\)
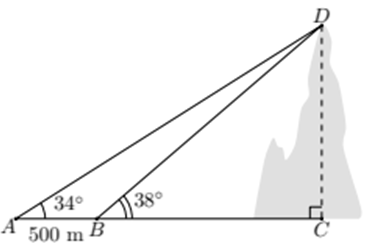
b) Đặt: \(BC = x\,\,\left( {\rm{m}} \right);\) \(AC = AB + BC = 500 + x\,\,\left( {\rm{m}} \right)\).
Xét \(\Delta ACD\) vuông tại \(C,\) ta có: \[CD = AC \cdot {\rm{tan}}\widehat {CAD} = \left( {500 + x} \right) \cdot {\rm{tan}}34^\circ .\]
Xét \(\Delta BCD\) vuông tại \(C,\) ta có: \(CD = BC \cdot {\rm{tan}}\widehat {CBD} = x \cdot {\rm{tan}}38^\circ \).
Do đó, ta có: \(\;\left( {500 + x} \right) \cdot {\rm{tan}}34^\circ = x \cdot {\rm{tan}}38^\circ \)
\(500 \cdot {\rm{tan}}34^\circ + x \cdot {\rm{tan}}34^\circ = x \cdot {\rm{tan}}38^\circ \)
\(\;x \cdot {\rm{tan}}38^\circ - x \cdot {\rm{tan}}34^\circ = 500 \cdot {\rm{tan}}34^\circ \)
\(\;x \cdot \left( {{\rm{tan}}38^\circ - {\rm{tan}}34^\circ } \right) = 500 \cdot {\rm{tan}}34^\circ \)
\(\;x = \frac{{500 \cdot {\rm{tan}}34^\circ }}{{{\rm{tan}}38^\circ - {\rm{tan}}34^\circ }} \approx 3\,\,158,5\,\,({\rm{m)}}{\rm{.}}\)
Suy ra \(CD = x \cdot {\rm{tan}}38^\circ \approx 3\,\,158,5 \cdot {\rm{tan}}38^\circ \approx 2468\,\,({\rm{m}}).\)
Vậy ngọn núi cao khoảng \(2\,\,468\) mét.
Câu 2
A. \[a \ge 60.\]
B. \[a < 60.\]
C. \[a = 60.\]
D. \[a > 60.\]
Lời giải
Đáp án đúng là: A
Do biển có hiệu lực bắt buộc các loại xe cơ giới vận hành với tốc độ không nhỏ hơn trị số ghi trên biển, nên theo hình vẽ thì tốc độ của ô tô đi trên đường đó không nhỏ hơn \[60{\rm{ km/h,}}\] tức là \[a \ge 60.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[\sin \beta = 0,5.\]
B. \[\cos \beta = 0,5.\]
C. \[\tan \beta = 0,5.\]
D. \[\cot \beta = 0,5.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo