Cho hình bình hành \[MNPQ\] có tâm \[O.\]
a) \[MN\] song song với \[PQ\] và \[MQ\] song song với \[NP.\]
b) Đoạn thẳng \[OM,{\rm{ }}ON\] lần lượt bằng đoạn thẳng \[OQ,{\rm{ }}OP.\]
c) Góc đỉnh \[M\] bằng góc đỉnh \[P.\]
d) Hình bình hành \[MNPQ\] có hai góc đỉnh \(M,\,\,N\) cùng bằng \(90^\circ \) thì \[MNPQ\] là hình chữ nhật.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: a) Đúng.b) Sai.c) Đúng.d) Đúng.
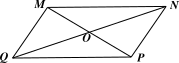
⦁ Vì \[MNPQ\] là hình bình hành nên \[MN\] song song với \[PQ\] và \[MQ\] song song với \[NP.\] Do đó ý a) là đúng.
⦁ Vì hình bình hành \[MNPQ\] có tâm \[O\] nên hai đường chéo \[MP,{\rm{ }}NQ\] cắt nhau tại trung điểm \[O\] của mỗi đường:
\[OM = OP\] và \[ON = OQ.\]
Đoạn thẳng \[OM,{\rm{ }}ON\] lần lượt bằng đoạn thẳng \[OP,{\rm{ }}OQ.\] Do đó ý b) là sai.
⦁ Vì \[MNPQ\] là hình bình hành nên góc đỉnh \[M\] bằng góc đỉnh \[P\] (hai góc đối diện bằng nhau). Do đó ý c) đúng.
⦁ Ta có hình bình hành \[MNPQ\] có góc đỉnh \[M\] bằng góc đỉnh \[P\] và góc đỉnh \[N\] bằng góc đỉnh \[Q\]
Mà hai góc đỉnh \(M,\,\,N\) cùng bằng \(90^\circ \) nên tất cả các góc của hình bình hành \[MNPQ\] đều bằng nhau và bằng \(90^\circ .\) Suy ra \[MNPQ\] là hình chữ nhật. Do đó ý d) đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Gọi \(x\) (quyển) là số sách mà trường THCS A bổ sung vào thư viện \(\left( {x \in \mathbb{N}*,\,\,x < 3\,\,000} \right).\)
Nếu xếp mỗi ngăn 26 quyển hoặc 50 quyển hoặc 65 quyển thì đều thừa 1 quyển nên ta có \[x\,\,:\,\,26\] dư 1, \(x\,\,:\,\,50\) dư 1, \(x\,\,:\,\,65\) dư 1.
Do đó \[\left( {x - 1} \right)\,\, \vdots \,\,26,\,\,\left( {x - 1} \right)\,\, \vdots \,\,50,\,\,\left( {x - 1} \right)\,\, \vdots \,\,65.\]
Như vậy, \[\left( {x - 1} \right) \in \]BC\(\left( {26,\,\,50,\,\,65} \right)\).
Ta có: \(26 = 2 \cdot 13;\,\,\,\,\,50 = 2 \cdot {5^2};\,\,\,\,\,65 = 5 \cdot 13.\)
Suy ra BCNN\(\left( {26,\,\,50,\,\,65} \right) = 2 \cdot {5^2} \cdot 13 = 650.\)
Nên BC\(\left( {26,\,\,50,\,\,65} \right) = \)B\[\left( {650} \right) = \left\{ {0;\,\,650;\,\,1\,\,300;\,\,1\,\,950;\,\,2\,\,600;\,\,3\,\,250;\,\,...} \right\}\].
Hay \[\left( {x - 1} \right) \in \left\{ {0;\,\,650;\,\,1\,\,300;\,\,1\,\,950;\,\,2\,\,600;\,\,3\,\,250;\,\,...} \right\}.\]
Khi đó \[x \in \left\{ {1;\,\,651;\,\,1\,\,301;\,\,1\,\,951;\,\,2\,\,601;\,\,3\,\,251;\,\,...} \right\}.\]
Mà \(x < 3\,\,000\) nên \[x \in \left\{ {1;\,\,651;\,\,1\,\,301;\,\,1\,\,951;\,\,2\,\,601} \right\}.\]
Theo bài, khi xếp số sách đó sao cho mỗi ngăn 17 quyển thì vừa đủ nên \(x\,\, \vdots \,\,17\). Trong các số tìm được ở trên, chỉ có số 2 601 chia hết cho 17 nên \(x = 2\,\,601.\)
Vậy trường THCS A đã bổ sung 2 601 quyển sách vào thư viện.
</></>
Câu 2
A. Toán.
B. Ngữ văn.
C. Tiếng Anh.
D. Khoa học tự nhiên.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
Qua hai học kì, điểm trung bình mỗi môn của chị An tăng như sau:
⦁ Môn Toán tăng: \(7,5 - 7 = 0,5\) (điểm).
⦁ Môn Ngữ văn tăng: \(8,2 - 7,8 = 0,4\) (điểm).
⦁ Môn Tiếng Anh tăng: \(8,3 - 8 = 0,3\) (điểm).
⦁ Môn Khoa học tự nhiên tăng: \(8,6 - 7,9 = 0,7\) (điểm).
Như vậy, môn Khoa học tự nhiên tăng nhiều nhất, tức môn Khoa học tự nhiên là môn mà chị An tiến bộ nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập