(0,5 điểm) Cho biểu thức \(A = - \frac{1}{3} + \frac{1}{{{3^2}}} - \frac{1}{{{3^3}}} + \frac{1}{{{3^4}}} - \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{100}}}}\). Tính giá trị của biểu thức \(B = 4\left| A \right| + \frac{1}{{{3^{100}}}}\).
Quảng cáo
Trả lời:
Hướng dẫn giải
Ta có: \(A = - \frac{1}{3} + \frac{1}{{{3^2}}} - \frac{1}{{{3^3}}} + \frac{1}{{{3^4}}} - \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{100}}}}\)
\(3A = - 1 + \frac{1}{3} - \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} - \frac{1}{{{3^4}}} + ... + \frac{1}{{{3^{99}}}}\)
Suy ra \(3A + A = - 1 + \frac{1}{3} - \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} - \frac{1}{{{3^4}}} + ... + \frac{1}{{{3^{99}}}} + \left( { - \frac{1}{3} + \frac{1}{{{3^2}}} - \frac{1}{{{3^3}}} + \frac{1}{{{3^4}}} - \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{100}}}}} \right)\)
\(4A = - 1 + \left( {\frac{1}{3} - \frac{1}{3}} \right) + \left( {\frac{1}{{{3^2}}} - \frac{1}{{{3^2}}}} \right) + \left( {\frac{1}{{{3^3}}} - \frac{1}{{{3^3}}}} \right) + \left( {\frac{1}{{{3^4}}} - \frac{1}{{{3^4}}}} \right) + ... + \left( {\frac{1}{{{3^{99}}}} - \frac{1}{{{3^{99}}}}} \right) + \frac{1}{{{3^{100}}}}\)
\(4A = - 1 + \frac{1}{{{3^{100}}}}\)
Suy ra \(A = \frac{1}{4}\left( { - 1 + \frac{1}{{{3^{100}}}}} \right)\).
Do \({3^{100}} > 1\) suy ra \(\frac{1}{{{3^{100}}}} < 1\) nên \(\frac{1}{{{3^{100}}}} - 1 < 0\) suy ra \(\frac{1}{4}\left( { - 1 + \frac{1}{{{3^{100}}}}} \right) < 0\) hay \(A < 0\).
Suy ra \(\left| A \right| = - A\).
Do đó, \(B = 4\left| A \right| + \frac{1}{{{3^{100}}}} = - 4A + \frac{1}{{{3^{100}}}} = - 4.\frac{1}{4}\left( {\frac{1}{{{3^{100}}}} - 1} \right) + \frac{1}{{{3^{100}}}}\)
\( = - \left( {\frac{1}{{{3^{100}}}} - 1} \right) + \frac{1}{{{3^{100}}}} = - \frac{1}{{{3^{100}}}} + 1 + \frac{1}{{{3^{100}}}} = 1 + \left( { - \frac{1}{{{3^{100}}}} + \frac{1}{{{3^{100}}}}} \right) = 1\).
Vậy \(B = 1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a)
|
GT |
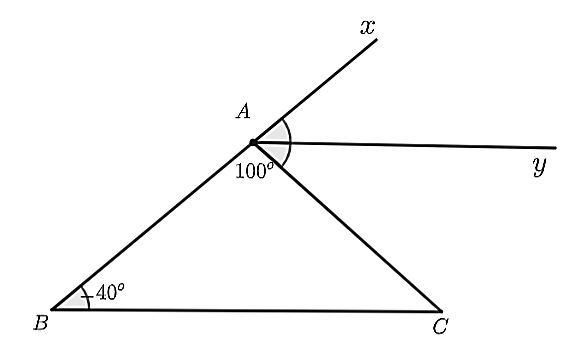
\(\widehat {xBC} = 40^\circ ,\widehat {BAC} = 100^\circ \); \(Ay\) là phân giác của \(\widehat {xAC}\); tia \(Az\) nằm trong \(\widehat {BAC}\); \(\widehat {zAy} = 90^\circ \) |
|
|
KL |
b) \(Ay\parallel BC\). c) tia \(Az\) là phân giác của \(\widehat {BAC}.\) |
b) Nhận thấy \(\widehat {BAC}\) và \(\widehat {CAx}\) là hai góc kề bù.
Do đó, ta có: \(\widehat {BAC} + \widehat {CAx} = 180^\circ \) nên \(\widehat {xAC} = 180^\circ - \widehat {BAC} = 180^\circ - 100^\circ = 80^\circ \).
Lại có \(Ay\) là tia phân giác của \(\widehat {xAC}\) nên \(\widehat {CAy} = \widehat {yAx} = \frac{{\widehat {CAx}}}{2} = \frac{{80^\circ }}{2} = 40^\circ \).
Suy ra \(\widehat {yAx} = \widehat {ABC} = 40^\circ \).
Mà hai góc ở vị trí đồng vị nên \(Ay\parallel BC\).
c)
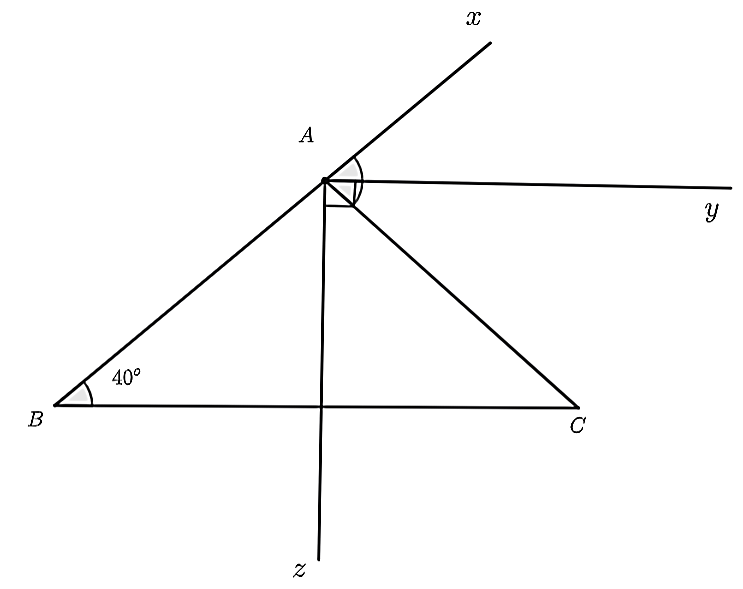
Nhận thấy \(\widehat {yAC}\) và \(\widehat {zAC}\) là hai góc kề nhau nên \(\widehat {zAC} + \widehat {yAC} = \widehat {zAy}\) hay \(\widehat {zAC} + 40^\circ = 90^\circ \).
Suy ra \(\widehat {zAC} = 90^\circ - 40^\circ = 50^\circ \).
Theo đề, tia \(Az\) nằm trong \(\widehat {BAC}\) nên \(\widehat {zAC}\) và \(\widehat {zAB}\) là hai góc kề nhau (1).
Do đó, \(\widehat {zAC} + \widehat {zAB} = \widehat {BAC}\) hay \(50^\circ + \widehat {zAB} = 100^\circ \) suy ra \(\widehat {zAB} = 100^\circ - 50 = 50^\circ \).
Suy ra \(\widehat {zAC} = \widehat {zAB} = 50^\circ \) (2).
Từ (1) và (2) suy ra tia \(Az\) là tia phân giác của \(\widehat {BAC}\).
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đb) Sc) Đc) S
• Thể tích của lòng thùng container là: \(5,8.3,2.2 = 37,12{\rm{ }}\left( {{{\rm{m}}^3}} \right)\). Do đó, ý a) là đúng.
• Thể tích của các thùng hàng là: \(50.40.20 = 40{\rm{ }}000\) (cm3).
Đổi \(40{\rm{ }}000{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right) = 0,04{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
Do đó, ý b) là sai.
• Số thùng hàng mà xe container có thể chở là: \(37,12:0,04 = 928\) (thùng).
Do đó, ý c) là đúng.
• Số tiền công mà xe nhận được là: \(\left( {928:10} \right).5{\rm{ }}000 = 464{\rm{ }}000\) (đồng).
Do đo, ý d) là sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.