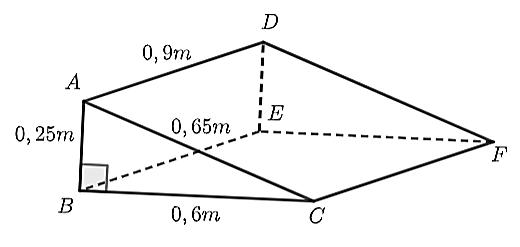
(1,0 điểm) Nhà ông An thuê thợ làm một cái gờ bằng bê tông để xe máy lên xuống bậc thềm có hình dạng giống như hình lăng trụ đứng tam giác như hình bên.

Biết \(AB = 0,25{\rm{ m;}}\) \(BC = 0,6{\rm{ m;}}\) \({\rm{ }}AC{\rm{ = 0,65 m;}}\)\(AD = 0,9{\rm{ m}}\). Đồng thời, tiền quét vôi tất cả các mặt của gờ là \(300{\rm{ 000}}\) đồng/m². Tính số tiền ông An cần trả để sơn tất cả các mặt của cái gờ.

Hướng dẫn giải

Đáp án: \(35\)

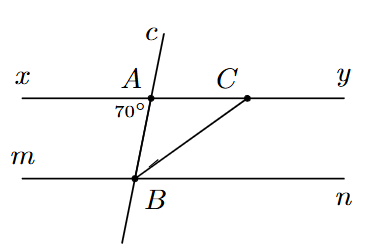
Vì

\(xy\parallel mn\) nên \(\widehat {xAB} = \widehat {ABn} = 70^\circ \) (so le trong).

Ta có tia \(BC\) là tia phân giác của \(\widehat {ABn}\) nên \(\widehat {ABC} = \widehat {CBn} = \widehat {\frac{{ABn}}{2}} = 35^\circ \).

Vì \(xy\parallel mn\) nên \(\widehat {ACB} = \widehat {CBn} = 35^\circ \).

Hướng dẫn giải

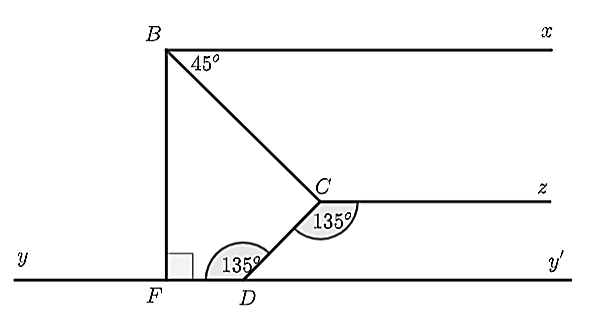
a) Nhận thấy, \(\widehat {FDC} = \widehat {DCz} = 135^\circ \) (giả thiết)

Mà hai góc ở vị trí so le trong nên \(Cz\parallel Dy.\)

Vì \(Dy\parallel Bx\) và \({\rm{ }}Dy \bot BF\) nên \({\rm{ }}Bx \bot BF\) tại \(B.\)

Suy ra \(\widehat {FBx} = 90^\circ \).

Nhận thấy \(\widehat {FBC}\) và \(\widehat {CBx}\) là hai góc kề nhau nên \(\widehat {FBC} + \widehat {CBx} = \widehat {FBx}\) hay \(\widehat {FBC} + 45^\circ = 90^\circ \).

Suy ra \(\widehat {FBC} = 90^\circ - 45^\circ = 45^\circ \).

Do đó, \(\widehat {FBC} = \widehat {CBx}\) và tia \(BC\) nằm giữa hai tia \(BF,Bx\) nên \(BC\) là tia phân giác của \(\widehat {FBx}.\)

b)

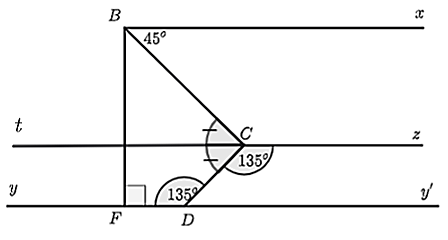
Có tia \(Ct\) là tia đối của tia \(Cz\) nên \(\widehat {tCz}\) là góc bẹt.

Có \(\widehat {tCD}\) và \(\widehat {DCz}\) là hai góc kề bù nên \(\widehat {tCD} + \widehat {DCz} = 180^\circ \) hay \(\widehat {tCD} + 135^\circ = 180^\circ \).

Suy ra \(\widehat {tCD} = 180^\circ - 135^\circ = 45^\circ \).

Vì \(Cz\parallel Dy\) và \(Dy\parallel Bx\) nên \(Cz\parallel Bx\). Do đó, \(Bx\parallel Ct\).

Suy ra \(\widehat {CBx} = \widehat {BCt} = 45^\circ \) (so le trong)

Do đó, \(\widehat {DCt} = \widehat {BCt} = 45^\circ \).

Mà \(Ct\) là tia nằm giữa hai tia \(CD\) và \(CB\).

Do đó, \(Ct\) là tia phân giác của \(\widehat {DCB}\).