Cho các hình vẽ sau:

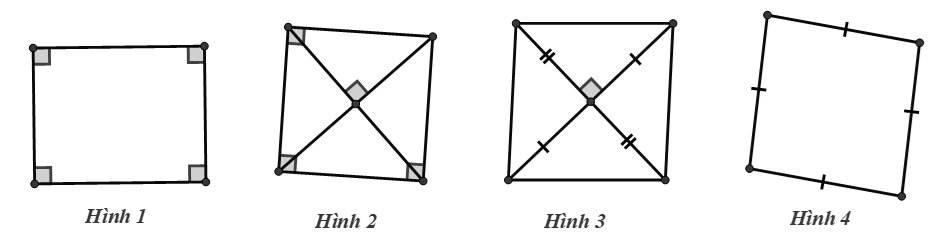
Trong các hình sau, những hình nào là hình vuông?

(1,5 điểm) Một cửa hàng sách cũ có một chính sách như sau: nếu khách hàng đăng kí làm hội viên của cửa hàng sách thì mỗi năm phải đóng \[50\,\,000\] đồng chi phí và chỉ phải mướn sách với giá \[5\,\,000\] đồng/cuốn sách, còn nếu khách hàng không phải hội viên thì sẽ mướn sách với giá \[10\,\,000\] đồng/cuốn sách. Gọi \[s\] (đồng) là tổng số tiền mỗi khách hàng phải trả trong mỗi năm và \[t\] là số cuốn sách mà khách hàng mướn.

a) Lập hàm số của

\[s\] theo \[t\] đối với khách hàng là hội viên và với khách hàng không phải là hội viên.

b) Trung là một hội viên của cửa hàng sách, năm ngoái thì Trung đã trả cho cửa hàng sách tổng cộng \[90\,\,000\] đồng. Hỏi nếu Trung không phải là hội viên của cửa hàng sách thì số tiền phải trả là bao nhiêu?

c) Một hội viên cần thuê tối thiểu bao nhiêu cuốn sách để có thể bù được phí hội viên?

Cho tam giác \[ABC\]. Dựng bên ngoài tam giác đó hai tam giác \[ABD,{\rm{ }}ACE\] vuông cân tại đỉnh \[A\] rồi dựng hình bình hành \[AEID\]. Biết \[\widehat {DAI} = \widehat {ABC}\]. Gọi \[K\] là trung điểm của \[BD.\]

a) \[\widehat {DAI} + \widehat {BAH} = 45^\circ \].b) \[AI \bot BC\].

c) \(\widehat {EBA} = \widehat {CDA}\).d) \[KA = \frac{1}{2}KB\].

Tứ giác \[ABCD\] có số đo các góc \[\widehat A\,,\,\,\widehat B\,,\,\,\widehat C\,,\,\,\widehat D\] tỉ lệ thuận với \[4\,;\,\,3\,;\,\,5\,;\,\,6.\] Tính số đo \[\widehat {A\,\,}\] theo đơn vị độ.

Cho biểu thức \[U = \frac{{5x + 1}}{{2x - 3}} \cdot \frac{{x + 2}}{{25{x^2} - 1}} - \frac{{8 - 3x}}{{25{x^2} - 1}}:\frac{{2x - 3}}{{5x + 1}}\,\,\,\left( {x \ne \frac{3}{2}\,;\,\,x \ne \frac{1}{5}\,;\,\,x \ne - \frac{1}{5}} \right)\].

Hỏi sau khi rút gọn biểu thức \[U\] ta được phân thức có tử thức bằng bao nhiêu?

Cho hình chóp tam giác đều \(S.ABC,\) có cạnh đáy \(AB = 5{\rm{\;cm}}\) và độ dài trung đoạn \(SI = 6{\rm{\;cm}}\) (hình vẽ bên). Tính diện tích xung quanh và diện tích toàn phần của hình chóp \(S.ABC.\)

Cho hai đa thức:

\(A = 2xy\left( {x{y^2} - 3{x^2}y + 1} \right)\) và \[B = \left( {12{x^4}{y^5} - 36{x^5}{y^4} + 6{x^3}{y^3}} \right):6{x^2}{y^2}.\]

Đa thức \(M\) thỏa mãn \(A = M + B.\)

a) Bậc của đa thức \[A\] là 8.

b) Hệ số tự do của đa thức \(B\) là 2.

c) Giá trị của biểu thức \(B\) tại \[x = - 1\,;\,\,y = 1\] là 12.

d) \(M\)là một đơn thức.

Khẳng định nào sau đây là sai?

Hướng dẫn giải