(1,0 điểm) Cho tam giác \[ABC\] vuông cân tại \(A.\) Lấy điểm \[M\] thuộc cạnh huyền \[BC.\] Gọi \[D,{\rm{ }}E\] lần lượt là hình chiếu của điểm \[M\] trên đường thẳng \[AB,{\rm{ }}AC.\]
a) Tứ giác \[ADME\] là hình gì? Vì sao?
b) Chứng minh khi điểm \[M\] thay đổi vị trí trên cạnh \[BC\] thì chu vi của tứ giác \[ADME\] không đổi.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
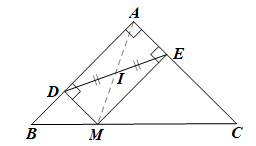
a)
Do \[D,{\rm{ }}E\] lần lượt là hình chiếu của điểm \[M\] trên đường thẳng \[AB,{\rm{ }}AC\] nên \[MD \bot AB,\] \[ME \bot AC.\]
Suy ra \[\widehat {ADM} = \widehat {AEM} = 90^\circ \]
Tam giác \[ABC\] vuông cân tại \[A\] nên \[\widehat {BAC} = 90^\circ .\]
Tứ giác \[ADME\] có \(\widehat {DAE} = \widehat {AEM} = \widehat {MDA} = 90^\circ \) nên \[ADME\] là hình chữ nhật.
b) Do \[ADME\] là hình chữ nhật nên \[DM\,{\rm{//}}\,AC.\]
Suy ra \(\widehat {BMD} = \widehat {ACB}\) (hai góc so le trong).
Mà \(\widehat {ABC} = \widehat {ACB} = 45^\circ \) (vì tam giác \[ABC\] vuông cân tại \[A),\] suy ra \(\widehat {BMD} = \widehat {ABC} = 45^\circ .\)
Do đó tam giác \[BDM\] cân tại \[D.\] Suy ra \[BD = DM.\]
Chu vi của hình chữ nhật \[ADME\] là: \[2\left( {AD + DM} \right) = 2\left( {AD + BD} \right) = 2AB.\]
Mà \[AB\] không đổi nên chu vi của tứ giác \[ADME\] không đổi.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án:
a) Đúng.
b) Sai.
c) Sai.
d) Đúng.
⦁ Tứ giác \(BMND\) có: \[MN\parallel BD{\rm{ }}\left( {MN\parallel BC} \right)\]; \[MN = BD\] (gt).
Do đó, tứ giác \(BMND\)là hình bình hành. Do đó ý a) là đúng.
⦁ Vì \(\Delta {\rm{ }}ABH\) vuông tại \(H\,\,\left( {AH \bot BC} \right)\) có \(HM\) là trung tuyến nên \(HM = \frac{1}{2}AB\).
Mà \(MA = \frac{1}{2}AB\) suy ra \(MA = HM\).
Vậy \(\Delta {\rm{ }}AMH\) cân tại \[M\]. Do đó ý b) sai.
⦁ Tứ giác \(DHMN\) có \[MN\parallel DH{\rm{ }}\left( {MN\parallel BC} \right)\] nên tứ giác \(DHMN\) là hình thang.\(\left( 1 \right)\)
Ta có \(AH \bot BC\); \[MN\parallel BC\] nên \(AH \bot MN\).
Vì \(\Delta {\rm{ }}AMH\) cân tại \[M\] có \(AH \bot MN\) nên \(MN\) là phân giác của \(\Delta {\rm{ }}AMH\).
Do đó \(\widehat {AMN} = \widehat {HMN}.\) Do đó ý c) sai.
⦁ Tứ giác \(BMND\)là hình bình hành nên \[ND\parallel MB\].
A. Do đó \(\widehat {AMN} = \widehat {DNM}\)(so le trong) nên \(\widehat {HMN} = \widehat {DNM}\).\(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra tứ giác \(DHMN\) là hình thang cân. Do đó ý d) đúng.
Lời giải
Hướng dẫn giải
Đáp số: 8040.
Đường cao mặt bên hình chóp chính là trung đoạn \[d = 67\;\;{\rm{mm}}\,{\rm{.}}\]
Diện tích xung quanh của khối rubik đó là:
\({S_{xq}} = \frac{1}{2} \cdot C \cdot d = \frac{1}{2} \cdot 180 \cdot 67 = 6030\;\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Đáy là tam giác đều có cạnh là \[180:3 = 60\;\;\left( {{\rm{cm}}} \right).\]
Chiều cao của tam giác đáy là \[67\;\;{\rm{cm}}\,{\rm{.}}\]
Diện tích toàn phần của khối rubik đó là:
\({S_{tp}} = 6030 + \frac{1}{2} \cdot 60 \cdot 67 = 8040\,\,\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Vậy diện tích toàn phần (tổng diện tích các mặt) của khối rubik đó là \(8040\,\,\;{\rm{c}}{{\rm{m}}^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo