Bảng 5 biều diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày.
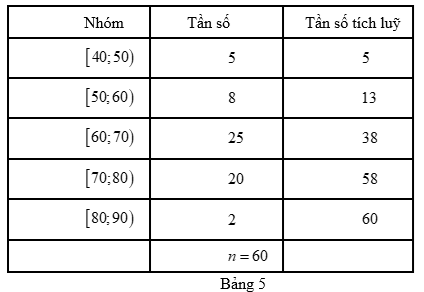 a) Số trung bình cộng của mẫu số liệu trên là \[65\] (nghìn đồng).
a) Số trung bình cộng của mẫu số liệu trên là \[65\] (nghìn đồng).
Bảng 5 biều diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày.

Quảng cáo
Trả lời:
a) Số trung bình cộng của mẫu số liệu ghép nhóm trên là
\(\overline x = \frac{{5.45 + 8.55 + 25.65 + 20.75 + 2.85}}{{60}} = 66\) (nghìn đồng)
Câu hỏi cùng đoạn
Câu 2:
b) Trung vị của mẫu số liệu trên là \[66,8\] (nghìn đồng).
b) Số phần tứ của mẫu là \(n = 60\). Ta có: \(\frac{n}{2} = \frac{{60}}{2} = 30\) mà \(13 < 30 < 38\). Suy ra nhóm \[3\] là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \[30\]. Xét nhóm \[3\] có \(r = 60\); \(d = 10; {n_3} = 25\) và nhóm \[2\] có \(c{f_2} = 13\).
Trung vị của mẫu số liệu đó là: \({M_e} = 60 + \left( {\frac{{30 - 13}}{{25}}} \right) \cdot 10 = 66,8\) (nghìn đồng).
Chọn đúng.
Câu 3:
c) Tứ phân vị nhất \({Q_1}\) của mẫu số liệu trên là \[60,8\] (nghìn đồng).
Tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đó là: \({Q_1} = 60 + \left( {\frac{{15 - 13}}{{25}}} \right) \cdot 10 = 60,8\) (nghìn đồng).
Chọn đúng
Câu 4:
d) Mốt của mẫu số liệu trên là \[65\] (nghìn đồng).
d) Ta thấy nhóm \[3\] là nhóm có tần số lớn nhất với \(u = 60; g = 10; {n_3} = 25\). Nhóm \[2\] có tần số \({n_2} = 8\), nhóm \[4\] có tần số \({n_4} = 20\).
Mốt của mẫu số liệu đó là: \({M_o} = 60 + \left( {\frac{{25 - 8}}{{2 \cdot 25 - 8 - 20}}} \right) \cdot 10 \approx 68\) (nghìn đồng).
Chọn sai
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn Sai
Lời giải
Khoảng biến thiên là \(R = 100 - 50 = 50\)
Kích thước của mẫu số liệu là \(N = 100\). Ta có \(\frac{N}{4} = 25;\frac{N}{2} = 50;\frac{{3N}}{4} = 75\).
- Đối với mẫu số liệu về điểm của lớp \(A\), ta tìm các tứ phân vị \(Q_1^A,Q_2^A,Q_3^A\) và khoảng tứ phân vị \(\Delta _Q^A\) qua bảng tần số tích luỹ dưới đây:
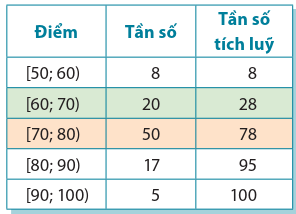
Nhóm chứa \(Q_1^A\) là \([60;70)\). \(Q_1^A = 60 + \frac{{25 - 8}}{{20}} \cdot 10 = 68,5\).
Nhóm chứa \(Q_2^A\) là [70 ; 80).\(Q_2^A = 70 + \frac{{50 - 28}}{{50}} \cdot 10 = 74,4\).
Nhóm chứa \(Q_3^A\) là [70 ; 80).\(Q_3^A = 70 + \frac{{75 - 28}}{{50}} \cdot 10 = 79,4\).
Vậy \(\Delta _Q^A = 79,4 - 68,5 = 10,9\).
Chọn đúng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.