Cho tam giác ABC với hai cạnh BC = 1cm, AC = 7cm.
Hãy tìm độ dài cạnh AB, biết rằng độ dài này là một số nguyên (cm). Tam giác ABC là tam giác gì?
Quảng cáo
Trả lời:
Theo bất đẳng thức tam giác ABC ta có:
AC – BC < AB < AC + BC
Thay BC = 1cm, AC = 7cm, ta được:
7 – 1 < AB < 7 + 1
6 < AB < 8 (1)
Vì độ dài AB là một số nguyên (cm) thỏa mãn (1) nên AB = 7cm
Do đó ΔABC cân tại A vì AB = AC = 7cm.
* Cách dựng tam giác ABC
- Vẽ BC = 1cm
- Dựng đường tròn tâm B bán kính 7cm ; đường tròn tâm C bán kính 7cm. Hai đường tròn cắt nhau tại A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
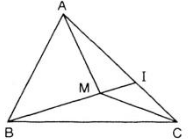
Theo giả thiết, điểm M nằm trong tam giác ABC nên điểm M không nằm trên cạnh AC.
⇒ A, M, I không thẳng hàng.
Xét bất đẳng thức tam giác trong ΔAMI:
MA < MI + IA
⇒ MA + MB < MB + MI + IA (cộng cả hai vế với MB)
hay MA + MB < IB + IA (vì MB + MI = IB).
Lời giải
Ta có : 4cm + 3cm = 7cm > 6cm.
⇒ Bộ ba đoạn thẳng 3cm, 4cm, 6cm thỏa mãn bất đẳng thức tam giác nên là ba cạnh của tam giác.
Cách dựng tam giác có ba độ dài 3cm, 4cm, 6cm
- Vẽ BC = 6cm
- Dựng đường tròn tâm B bán kính 3cm ; đường tròn tâm C bán kính 4cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.