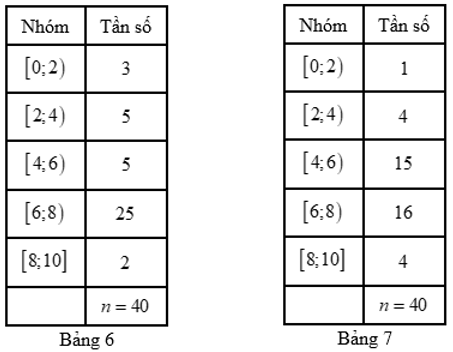
Kết quả kiểm tra môn Tiếng Anh (cùng đề) của học sinh hai lớp \(12A\) và \[12B\] được cho lần lượt bời mẫu số liệu ghép nhóm ở Bảng 6, Bảng 7.

a) Số trung bình cộng của hai mẫu số liệu trên bằng nhau.

Phương sai của mẫu số liệu lớp \(12A\) là:

\(s_A^2 = \frac{{3{{\left( {1 - 5,9} \right)}^2} + 5{{\left( {3 - 5,9} \right)}^2} + 5{{\left( {5 - 5,9} \right)}^2} + 25{{\left( {7 - 5,9} \right)}^2} + 2{{\left( {9 - 5,9} \right)}^2}}}{{40}} = 4,19.\)

Độ lệch chuẩn của mẫu số liệu lớp \(12A\) là \(\sqrt {4,19} \) và \(\sqrt {4,19}  > 2\).

Phương sai của mẫu số liệu lớp \(12B\) là:

\(s_B^2 = \frac{{1{{\left( {1 - 5,9} \right)}^2} + 4{{\left( {3 - 5,9} \right)}^2} + 15{{\left( {5 - 5,9} \right)}^2} + 16{{\left( {7 - 5,9} \right)}^2} + 4{{\left( {9 - 5,9} \right)}^2}}}{{40}} = 3,19\)

Và \(3,19 > 3\).

Chọn Đúng

Số trung bình cộng của mẫu số liệu lớp \(12A\) là:

\({\rm{\;}}\overline {{x_A}}  = \frac{{3.1 + 5.3 + 5.5 + 25.7 + 2.9}}{{40}} = 5,9.\)

Số trung bình cộng của mẫu số liệu lớp \[12B\] là:

\(\overline {{x_B}}  = \frac{{1.1 + 4 \cdot 3 + 15.5 + 16 \cdot 7 + 4.9}}{{40}} = 5,9.\)

Suy ra số trung bình cộng của hai mẫu số liệu trên bằng nhau.

Phương sai của mẫu số liệu lớp \(12A\) là:

\(s_A^2 = \frac{{3{{\left( {1 - 5,9} \right)}^2} + 5{{\left( {3 - 5,9} \right)}^2} + 5{{\left( {5 - 5,9} \right)}^2} + 25{{\left( {7 - 5,9} \right)}^2} + 2{{\left( {9 - 5,9} \right)}^2}}}{{40}} = 4,19.\)

Độ lệch chuẩn của mẫu số liệu lớp \(12A\) là \(\sqrt {4,19} \) và \(\sqrt {4,19}  > 2\).

Phương sai của mẫu số liệu lớp \(12B\) là:

\(s_B^2 = \frac{{1{{\left( {1 - 5,9} \right)}^2} + 4{{\left( {3 - 5,9} \right)}^2} + 15{{\left( {5 - 5,9} \right)}^2} + 16{{\left( {7 - 5,9} \right)}^2} + 4{{\left( {9 - 5,9} \right)}^2}}}{{40}} = 3,19\)

Và \(3,19 > 3\).

Vì \(s_A^2 > s_B^2\) nên điểm thi của học sinh lớp \(12B\) đồng đều hơn lớp \(12A\).