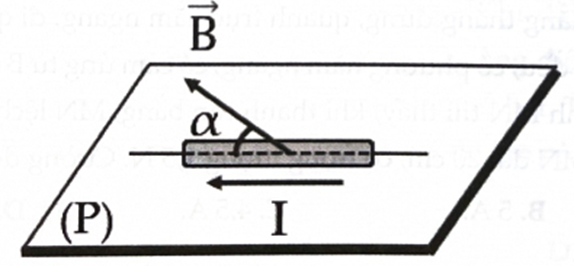
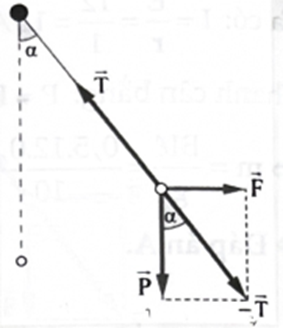
Treo đoạn dây dẫn có chiều dài \(\ell \) = 10 cm; khối lượng m = 5 g bằng hai dây mảnh, nhẹ sao cho dây dẫn nằm ngang. Biết cảm ứng từ của từ trường hướng thẳng đứng lên trên (hình bên), có độ lớn B = 0,05 T và dòng điện chạy qua dây dẫn là \({\rm{I}} = 10\sqrt 3 \;{\rm{A}}.\) Nếu lấy g = 10 m/s2 thì góc lệch a của dây treo so với phương thẳng đứng là
A. 60°.
B. 30°.
C. 15°.
D. 45°.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \(\tan \alpha = \frac{{\rm{F}}}{{\rm{P}}} = \frac{{{\rm{BI}}\ell }}{{{\rm{mg}}}} = \frac{{0,05 \cdot 10\sqrt 3 \cdot 0,1}}{{5 \cdot {{10}^{ - 3}} \cdot 10}} = \sqrt 3 \Rightarrow \alpha = {60^^\circ }\)
Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\[F = IB\ell \sin \alpha \Rightarrow B = \frac{F}{{I\ell \sin \alpha }} = \frac{{{{3.10}^{ - 3}}}}{{0,75.0,05.\sin 90^\circ }} = 0,08\,T.\] Chọn B.
Câu 2
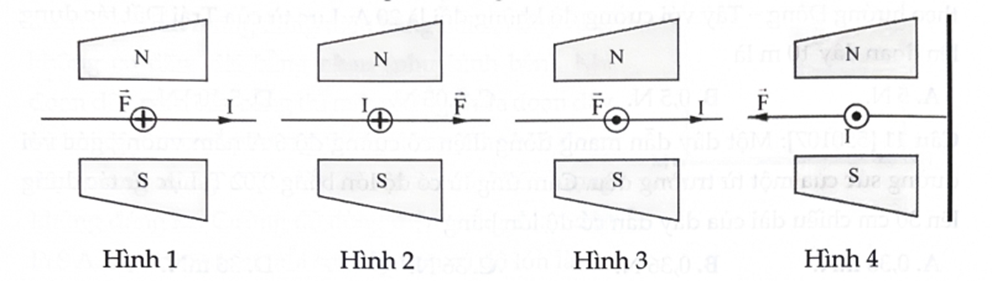
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Lời giải
Sử dụng quy tắc bàn tay trái. Chọn A.
Câu 3
A. vuông góc với đoạn dây dẫn.
B. cùng hướng với vectơ cảm ứng từ.
C. vuông góc với vectơ cảm ứng từ.
D. vuông góc cả đoạn dây dẫn và vectơ cảm ứng từ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(0,4\sqrt 3 \;{\rm{N}}.\)
B. \(0,4\;{\rm{N}}.\)
C. \(0,8\;{\rm{N}}.\)
D. \(\frac{{0,8}}{{\sqrt 3 }}\;{\rm{N}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. cùng hướng với hướng của từ trường tại điểm đó.
B. cùng hướng với lực từ tác dụng lên phần tử dòng điện đặt tại điểm đó.
C. có độ lớn tỉ lệ nghịch với độ lớn của lực từ tác dụng lên phần tử dòng điện đặt tại điểm đó.
D. có độ lớn tỉ lệ với cường độ của phần tử dòng điện đặt tại điểm đó.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập