Tìm nghiệm lớn nhất của phương trình \(2\cos 2x - 1 = 0\) trong đoạn \(\left[ {0;\pi } \right]\).
Tìm nghiệm lớn nhất của phương trình \(2\cos 2x - 1 = 0\) trong đoạn \(\left[ {0;\pi } \right]\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương trình \(2\cos 2x - 1 = 0\)\( \Leftrightarrow \cos 2x = \frac{1}{2}\) \( \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{3} + k2\pi \\2x = - \frac{\pi }{3} + k2\pi \end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = - \frac{\pi }{6} + k\pi \end{array} \right.,k \in \mathbb{Z}\).
Xét \(x \in \left[ {0;\pi } \right]\) \( \Leftrightarrow \left[ \begin{array}{l}0 \le \frac{\pi }{6} + k\pi \le \pi \\0 \le - \frac{\pi }{6} + k\pi \le \pi \end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\frac{{ - 1}}{6} \le k \le \frac{5}{6}\\\frac{1}{6} \le k \le \frac{7}{6}\end{array} \right.\) mà \(k \in \mathbb{Z}\) suy ra \(\left[ \begin{array}{l}k = 0\\k = 1\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6}\\x = \frac{{5\pi }}{6}\end{array} \right.\).
Vậy nghiệm lớn nhất của phương trình \(2\cos 2x - 1 = 0\) trong đoạn \(\left[ {0;\pi } \right]\) là \(x = \frac{{5\pi }}{6}\).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
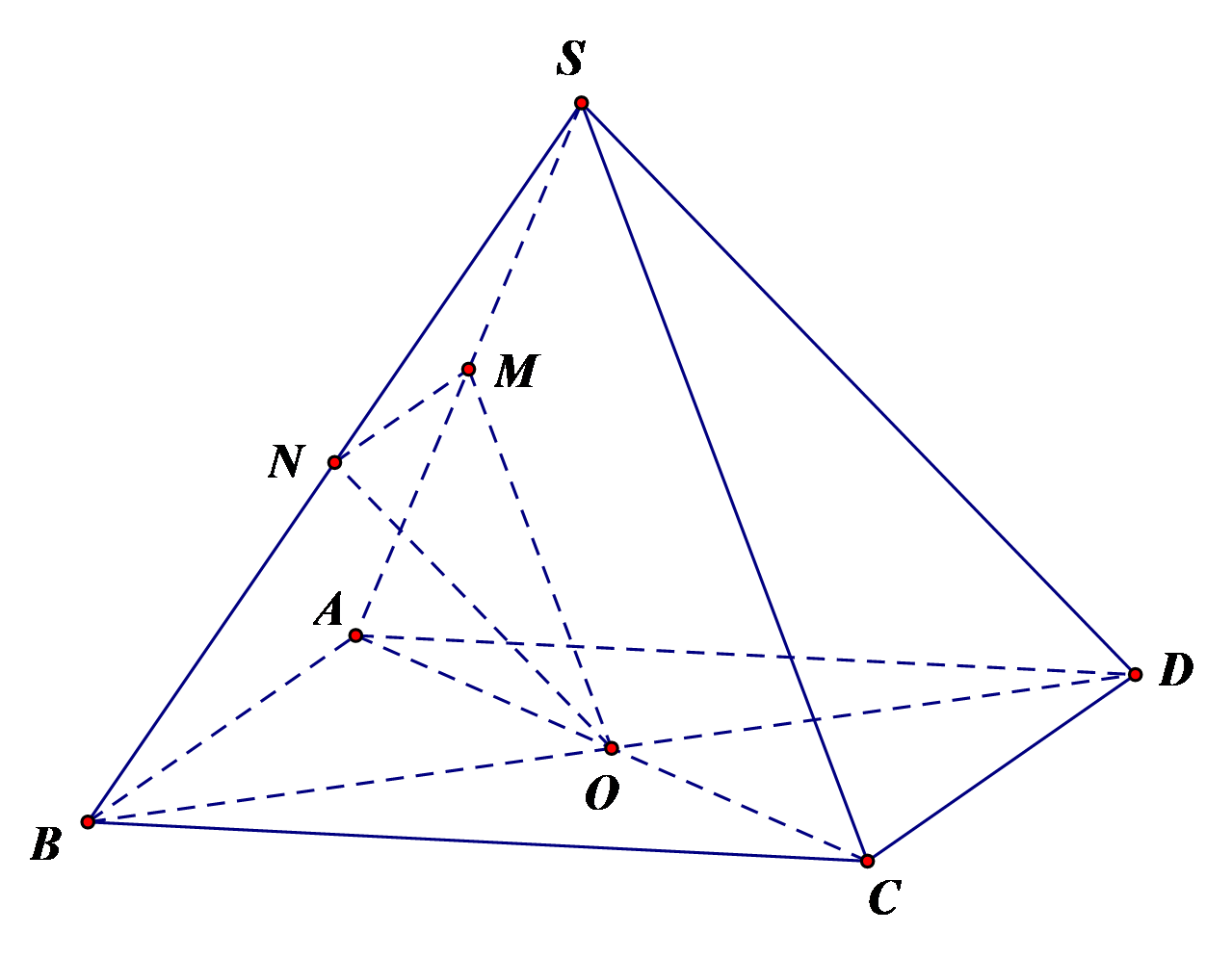
a) Ta có M Î SA, N Î SB nên MN Ì (SAB).
b) Ta có M là trung điểm SA, O là trung điểm AB.
Suy ra MO là đường trung bình của DSAC Þ MO // SC.
Mà SC Ì (SBC) Þ MO // (SBC).
c) Ta có N Î SB, O Î BD nên NO Ì (SBD).
d) Ta có M, N lần lượt là trung điểm của SA, SB nên MN // AB
Mà AB // CD nên MN // CD.
Lại có MN Ì (MNO) Þ CD // (MNO).
Đáp án: a) Sai; b) Đúng; c) Sai; d) Đúng.
Câu 2
A. \(MP\,{\rm{//}}\,\left( {BCD} \right)\).
B. \(GQ\,{\rm{//}}\,\left( {BCD} \right)\).
C. \(MP \subset \) \(\left( {BCD} \right)\).
D. \(Q\) thuộc mặt phẳng \(\left( {CDP} \right)\).
Lời giải
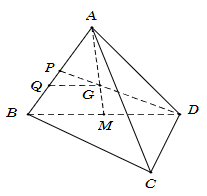
Vì \(G\) là trọng tâm tam giác \[ABD\] nên \(\frac{{AG}}{{AM}} = \frac{2}{3}\).
Điểm \(Q \in AB\) sao cho \(AQ = 2QB\) suy ra \(\frac{{AQ}}{{AB}} = \frac{2}{3}\).
Khi đó \(\frac{{AG}}{{AM}} = \frac{{AQ}}{{AB}} = \frac{2}{3}\), theo định lí Thalès đảo ta có \(QC\,{\rm{//}}\,BD\).
Mặt khác \[BD\] nằm trong mặt phẳng \(\left( {BCD} \right)\) suy ra \[GQ\,{\rm{//}}\,\left( {BCD} \right)\]. Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(d\,{\rm{//}}\,d'\).
B. \(d\) cắt \(d'\).
C. \(d\) và \(d'\) chéo nhau.
D. \(d \equiv d'\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(a\,{\rm{//}}\,b\) và \(b \subset \left( P \right)\).
B. \(a\,{\rm{//}}\,b\) và \(b\,{\rm{//}}\,\left( P \right)\).
C. \(a \subset \left( Q \right)\) và \(b \subset \left( P \right)\).
D. \(a\,{\rm{//}}\,b\); \(a \subset \left( Q \right)\) và \(b \subset \left( P \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo