Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = \cos x\).
a) Hàm số đã cho có tập xác định là \(D = \left[ { - 1;1} \right]\).
b) Đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
c) Đồ thị hàm số đã cho nhận trục tung làm trục đối xứng.
d) Hàm số đã cho nghịch biến trên khoảng \(\left( {0;\frac{{3\pi }}{2}} \right)\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = \cos x\).
a) Hàm số đã cho có tập xác định là \(D = \left[ { - 1;1} \right]\).
b) Đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
c) Đồ thị hàm số đã cho nhận trục tung làm trục đối xứng.
d) Hàm số đã cho nghịch biến trên khoảng \(\left( {0;\frac{{3\pi }}{2}} \right)\).
Quảng cáo
Trả lời:
a) Hàm số \(y = \cos x\) có tập xác định \(D = \mathbb{R}\).
b) Thay tọa độ điểm \(A\left( {0;1} \right)\)vào hàm số \(y = \cos x\) thỏa mãn.
c) Hàm số \(y = \cos x\) chẵn nhận trục tung làm trục đối xứng.
d) Hàm số đã cho nghịch biến trên khoảng \(\left( {0;\pi } \right)\).
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] \ge - 1\) \( \Rightarrow 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12 \ge 9\)\( \Rightarrow d\left( t \right) \ge 9\).
Vậy thành phố T có ít giờ có ánh sáng mặt trời nhất khi vào chỉ khi \(\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = - 1\)
\( \Leftrightarrow \frac{\pi }{{182}}\left( {t - 80} \right) = - \frac{\pi }{2} + k2\pi \)\( \Leftrightarrow t - 80 = 182\left( { - \frac{1}{2} + k2} \right)\)\( \Leftrightarrow t = 364k - 11,k \in \mathbb{Z}\).
Mặt khác \(0 \le 364k - 11 \le 365\)\( \Leftrightarrow \frac{{11}}{{364}} \le k \le \frac{{376}}{{364}}\)\( \Leftrightarrow k = 1\) (do \(k \in \mathbb{Z}\)).
Suy ra \(t = 364 - 11 = 353\).
Vậy thành phố T có ít giờ ánh sáng Mặt Trời nhất là 9 giờ khi t = 353, tức là vào ngày thứ 353 trong năm.
Trả lời: 353.
Câu 2
Cho hàm số \(y = \sin x\) có đồ thị như hình
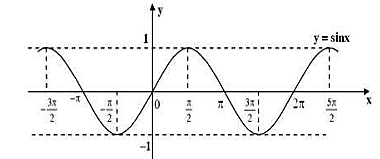
a) Hàm số \(y = \sin x\) nghịch biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\) và đồng biến trên khoảng \(\left( {\frac{\pi }{2};\pi } \right)\).
b) Trên khoảng \(\left( { - \frac{\pi }{2};\frac{{5\pi }}{2}} \right)\) có 3 giá trị của \(x\) để \(\sin x = 0\).
c) Đường thẳng \(y = - 0,35\) giao với đồ thị hàm số \(y = \sin x\) tại 2 điểm phân biệt trên khoảng \(\left( { - \frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
d) Hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( {\frac{\pi }{7};\frac{\pi }{5}} \right)\).
Cho hàm số \(y = \sin x\) có đồ thị như hình

a) Hàm số \(y = \sin x\) nghịch biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\) và đồng biến trên khoảng \(\left( {\frac{\pi }{2};\pi } \right)\).
b) Trên khoảng \(\left( { - \frac{\pi }{2};\frac{{5\pi }}{2}} \right)\) có 3 giá trị của \(x\) để \(\sin x = 0\).
c) Đường thẳng \(y = - 0,35\) giao với đồ thị hàm số \(y = \sin x\) tại 2 điểm phân biệt trên khoảng \(\left( { - \frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
d) Hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( {\frac{\pi }{7};\frac{\pi }{5}} \right)\).
Lời giải
a) Hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\) và nghịch biến trên khoảng \(\left( {\frac{\pi }{2};\pi } \right)\).
b) Trên khoảng \(\left( { - \frac{\pi }{2};\frac{{5\pi }}{2}} \right)\), đường thẳng \(y = 0\) cắt đồ thị hàm số \(y = \sin x\) tại 3 điểm phân biệt nên có 3 giá trị của \(x\) để \(\sin x = 0\).
c) Trên khoảng \(\left( { - \frac{\pi }{2};\frac{{3\pi }}{2}} \right)\), đường thẳng \(y = - 0,35\) cắt đồ thị hàm số \(y = \sin x\) tại 2 điểm phân biệt.
d) Dựa vào đồ thị hàm số ta có hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( {\frac{\pi }{7};\frac{\pi }{5}} \right)\).
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
