Miền không bị gạch chéo (kể cả các đường thẳng) là miền nghiệm của hệ bất phương trình nào?
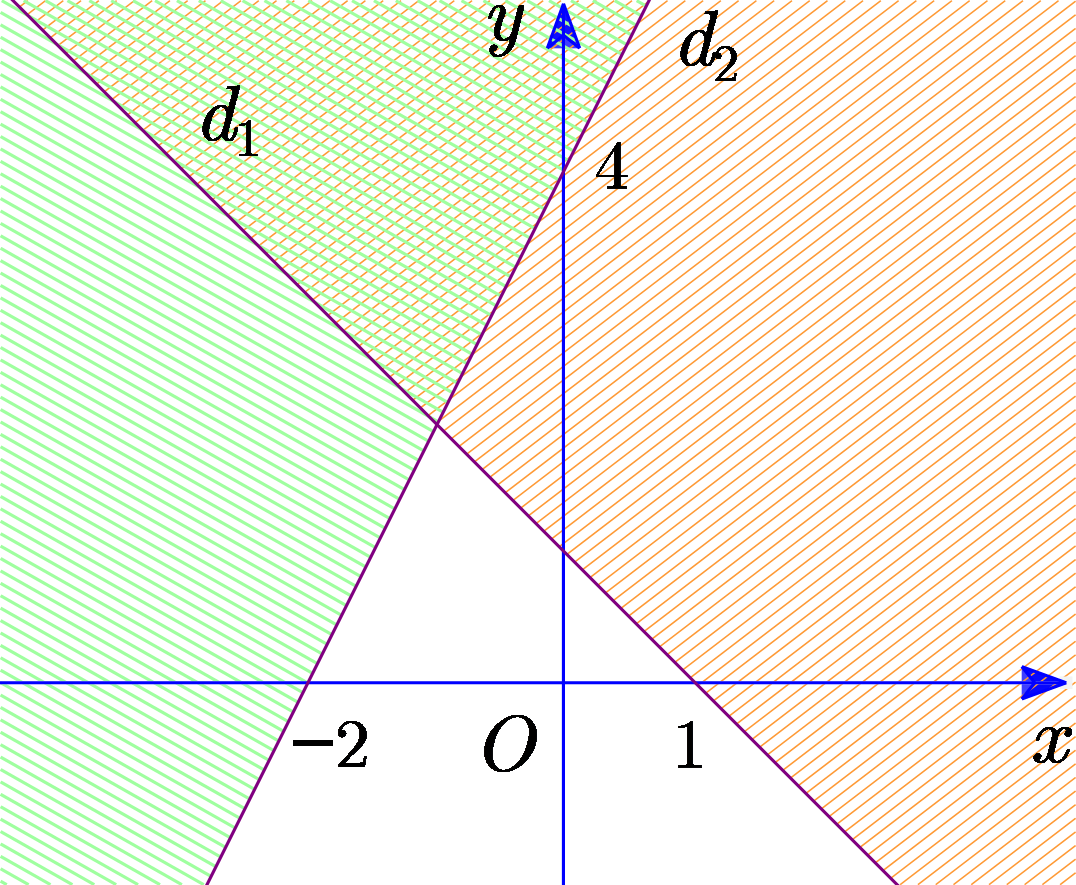
Miền không bị gạch chéo (kể cả các đường thẳng) là miền nghiệm của hệ bất phương trình nào?

Quảng cáo
Trả lời:
Đường thẳng d1 đi qua điểm (1; 0) và (0; 1) có phương trình là \(x + y - 1 = 0\).
Vì O(0; 0) không thuộc d1 thuộc vào miền nghiệm nên thay (0; 0) vào d1 ta có \( - 1 < 0\).
Suy ra \(x + y - 1 \le 0\).
Đường thẳng d2 đi qua điểm (−2; 0) và (0; 4) có phương trình \(2x - y + 4 = 0\).
Vì O(0; 0) không thuộc d2 thuộc miền nghiệm nên thay (0; 0) vào d2 ta có 4 > 0.
Suy ra \(2x - y + 4 \ge 0\).
Vậy miền không bị gạch chéo là miền nghiệm của bất phương trình \(\left\{ \begin{array}{l}x + y - 1 \le 0\\2x - y + 4 \ge 0\end{array} \right.\). Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Nhân ngày tết trung thu, một rạp chiếu phim phục vụ khán giả một bộ phim hoạt hình. Vé bán ra có hai loại:
Loại 1 (dành cho trẻ từ 6 – 13 tuổi): 50000 đồng/vé.
Loại 2 (dành cho người trên 13 tuổi): 100000 đồng/vé.
Người ta tính toán rằng nếu bán được \(x\) vé loại 1 và \(y\) vé loại 2, để không phải bù lỗ thì số tiền vé thu được phải đạt tối thiểu 20 triệu đồng.
a) Số tiền bán được của vé loại 1 là \(50000x\), số tiền bán được của vé loại 2 là \(100000y\) với điều kiện \(x \ge 0;y \ge 0\).
b) Bất phương trình biểu thị mối liên hệ giữa \(x\) và \(y\) để rạp phim không bị lỗ là \(50x + 100y \le 20000\).
c) \(\left( {200;100} \right)\) là một nghiệm của bất phương trình bậc nhất \(50x + 100y \ge 20000\).
d) Miền nghiệm của bất phương trình \(50x + 100y \ge 20000\) là nửa mặt phẳng bờ là đường thẳng \(d:50x + 100y = 20000\) không chứa điểm \(O\left( {0;0} \right)\).
Nhân ngày tết trung thu, một rạp chiếu phim phục vụ khán giả một bộ phim hoạt hình. Vé bán ra có hai loại:
Loại 1 (dành cho trẻ từ 6 – 13 tuổi): 50000 đồng/vé.
Loại 2 (dành cho người trên 13 tuổi): 100000 đồng/vé.
Người ta tính toán rằng nếu bán được \(x\) vé loại 1 và \(y\) vé loại 2, để không phải bù lỗ thì số tiền vé thu được phải đạt tối thiểu 20 triệu đồng.
a) Số tiền bán được của vé loại 1 là \(50000x\), số tiền bán được của vé loại 2 là \(100000y\) với điều kiện \(x \ge 0;y \ge 0\).
b) Bất phương trình biểu thị mối liên hệ giữa \(x\) và \(y\) để rạp phim không bị lỗ là \(50x + 100y \le 20000\).
c) \(\left( {200;100} \right)\) là một nghiệm của bất phương trình bậc nhất \(50x + 100y \ge 20000\).
d) Miền nghiệm của bất phương trình \(50x + 100y \ge 20000\) là nửa mặt phẳng bờ là đường thẳng \(d:50x + 100y = 20000\) không chứa điểm \(O\left( {0;0} \right)\).
Lời giải
a) Số tiền bán được của vé loại 1 là \(50000x\), số tiền bán được của vé loại 2 là \(100000y\) với điều kiện \(x \ge 0;y \ge 0\).
b) Bất phương trình biểu thị mối liên hệ giữa \(x\) và \(y\) để rạp phim không bị lỗ là:
\(50000x + 100000y \ge 20000000\)\( \Leftrightarrow 50x + 100y \ge 20000\).
c) Thay \(x = 200;y = 100\) vào bất phương trình \(50x + 100y \ge 20000\) ta thấy thoả mãn.
Vậy \(\left( {200;100} \right)\) là một nghiệm của bất phương trình bậc nhất \(50x + 100y \ge 20000\).
d) Thay điểm (0; 0) vào bất phương trình ta thấy không thỏa mãn.
Do đó miền nghiệm của bất phương trình \(50x + 100y \ge 20000\) là nửa mặt phẳng bờ là đường thẳng \(d:50x + 100y = 20000\) không chứa điểm \(O\left( {0;0} \right)\).
Đáp án: a) Đúng; b) Sai; c) Đúng; d) Đúng.
Câu 2
Lời giải
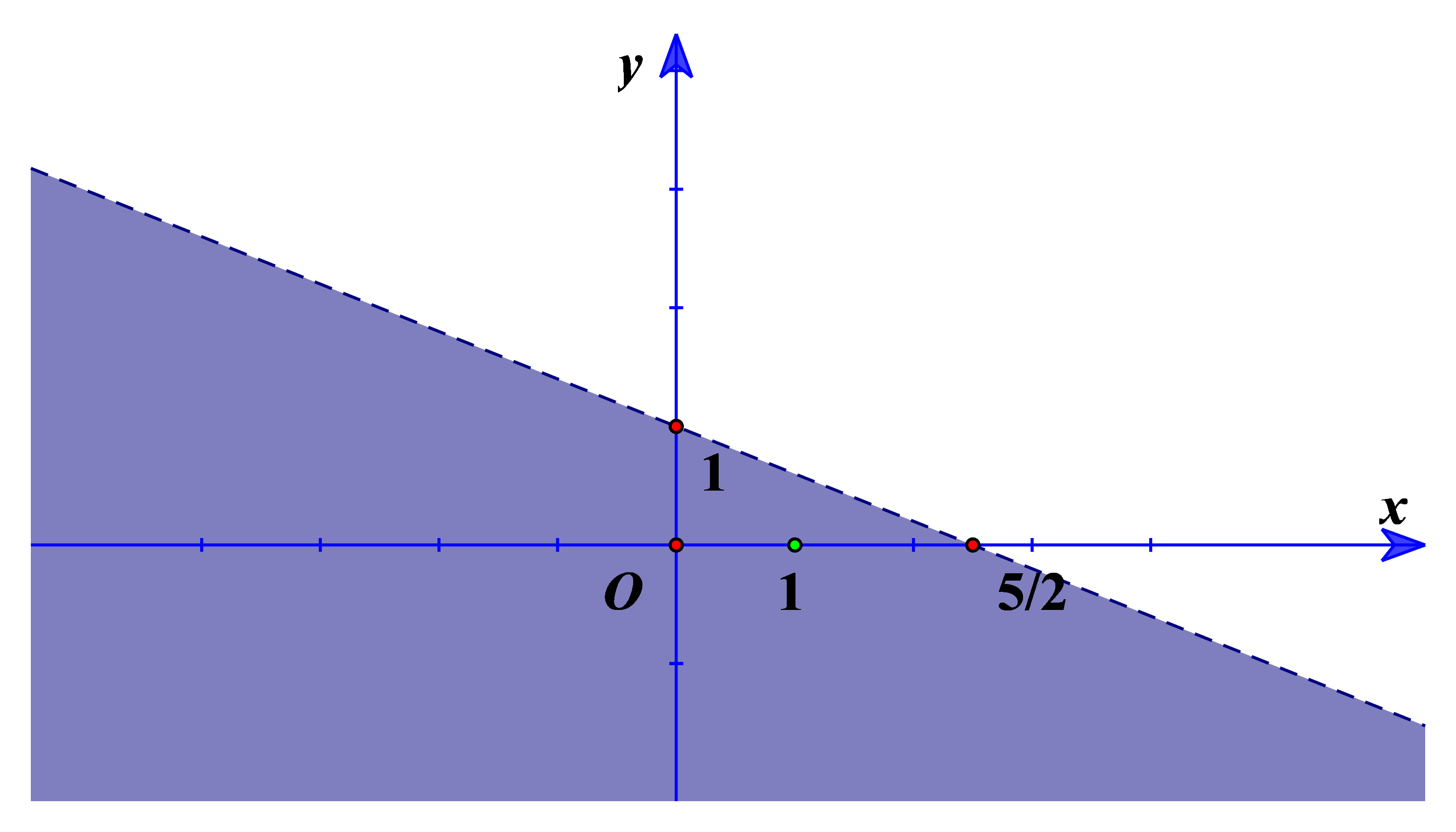
Đường thẳng d đi qua điểm (1; 0) và (0; −1) có phương trình là \(x - y = 1\).
Điểm O(0; 0) không thuộc d thuộc miền nghiệm của bất phương trình nên hình trên là miền nghiệm của bất phương trình có dạng \(x - y \le 1\). Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
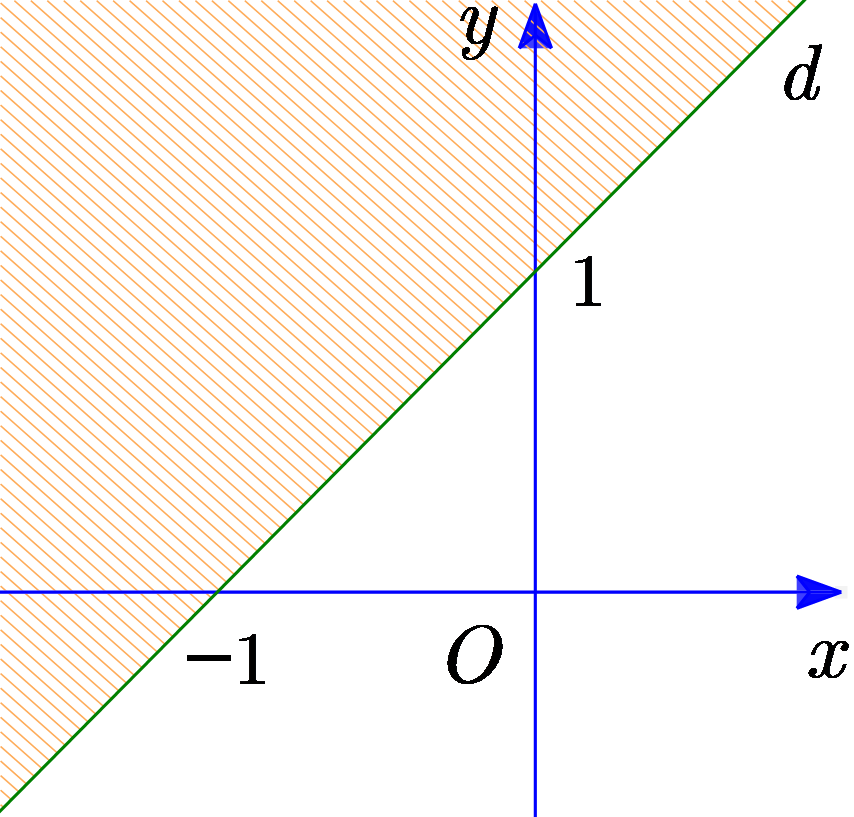
![Miền không gạch chéo (không kể bờ \(d\)) trong hình sau là miền nghiệm của bất phương trình nào trong các bất phương trình dưới đây? A. \[x + 2y < 4\]. B. \[2x + y \ge 4\]. C. \[x + 2y \ge 4\]. D. \[x + 2y > 4\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/4-1758596000.png)