Cho x và y thoả mãn: \({x^2} + 5{y^2} - 3xy - 3x - y + 5 = 0\). Tính giá trị của biểu thức:
\(A = \frac{{{{\left( {x + y - 4} \right)}^{2222}} - {y^{2222}}}}{x}.\)
Cho x và y thoả mãn: \({x^2} + 5{y^2} - 3xy - 3x - y + 5 = 0\). Tính giá trị của biểu thức:
\(A = \frac{{{{\left( {x + y - 4} \right)}^{2222}} - {y^{2222}}}}{x}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Ta có: \({x^2} + 5{y^2} - 3xy - 3x - y + 5 = 0\)
Suy ra \(2{x^2} + 10{y^2} - 6xy - 6x - 2y + 10 = 0\)
\({x^2} - 6xy + 9{y^2} + {x^2} - 6x + 9 + {y^2} - 2y + 1 = 0\)
\(\left( {{x^2} - 6xy + 9{y^2}} \right) + \left( {{x^2} - 6x + 9} \right) + \left( {{y^2} - 2y + 1} \right) = 0\)
\({\left( {x - 3y} \right)^2} + {\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 0\)
Với mọi \(x,\,\,y\) ta có: \({\left( {x - 3y} \right)^2} \ge 0,\,\,{\left( {x - 3} \right)^2} \ge 0,\,\,{\left( {y - 1} \right)^2} \ge 0\)
Suy ra \({\left( {x - 3y} \right)^2} + {\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} \ge 0\)
Do đó, để \({\left( {x - 3y} \right)^2} + {\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 0\) thì \[\left\{ {\begin{array}{*{20}{l}}{{{\left( {x - 3y} \right)}^2} = 0}\\{{{\left( {x - 3} \right)}^2} = 0}\\{{{\left( {y - 1} \right)}^2} = 0}\end{array}} \right.\] hay \(\left\{ {\begin{array}{*{20}{l}}{x - 3y = 0}\\{x - 3 = 0}\\{y - 1 = 0}\end{array}} \right.\), tức là \(\left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 1}\end{array}} \right.\).
Thay \(x = 3,\,\,y = 1\) vào biểu thức \(A,\) ta được:
\[A = \frac{{{{\left( {3 + 1 - 4} \right)}^{2222}} - {1^{2222}}}}{3} = \frac{{ - 1}}{3}.\]
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
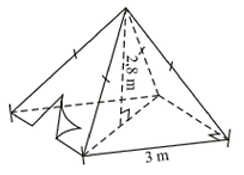
a) Diện tích đáy hình vuông của chiếc lều là:
Thể tích không khí bên trong chiếc lều là:
b) Diện tích xung quanh của chiếc lều là:
\({S_{xq}} = \frac{1}{2} \cdot C \cdot d = \frac{1}{2} \cdot \left( {4 \cdot 3} \right) \cdot 3,18 = 19,08{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích vải phủ bốn phía và trải nền đất cho chiếc lều là:
\(S = 9 + 19,08 = 28,08\) (m2).
Do \(28,08 > 20\) nên số tiền mua vải được giảm giá \(5\% \) trên tổng hóa đơn.
Vậy số tiền mua vải là: \(28,08 \cdot 15\,\,000 \cdot \left( {100\% - 5\% } \right) = 400\,\,140\) (đồng).
Lời giải
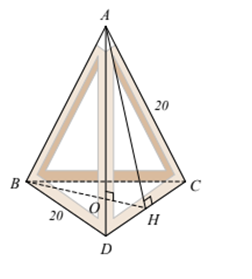
a) Chiếc đèn được mô phỏng thành hình chóp tam giác đều \(A.BCD\) như hình vẽ. Gọi \(AH\) là trung đoạn kẻ từ đỉnh \(A\) của hình chóp.
Theo bài ta có: \(AB = AC = AD = 20\) cm và \(BC = CD = DB = 20\) cm.
\(\Delta ACD\) đều nên \(AH\) vừa là đường cao vừa là đường trung tuyến.
Do đó \(DH = CH = \frac{1}{2}CD = 10\) cm.
Xét \(\Delta AHC\) vuông tại \(H\), áp dụng định lí Pythagore ta có:
\(A{H^2} = A{C^2} - C{H^2} = {20^2} - {10^2} = 300\)
Suy ra \(AH = \sqrt {300} = \sqrt {100.3} = \sqrt {{{\left( {10\sqrt 3 } \right)}^2}} = 10\sqrt 3 \) cm.b) Chu vi đáy của hình chóp là: \({C_{day}} = 3BD = 3.20 = 60\) cm.
Diện tích xung quanh của chiếc đèn là:
\({S_{xq}} = \frac{1}{2}{C_{day}}.AH = \frac{1}{2}.60.10\sqrt 3 = 300\sqrt 3 \) cm2.
c) Vì \(\Delta ADC\) và \(\Delta BDC\) đều là các tam giác đều có cạnh 20 cm nên hai đường cao \(AH\) và \(BH\) của hai tam giác bằng nhau.
Vì \(O\) là trọng tâm \(\Delta BDC\) nên \(OH = \frac{1}{3}BH = \frac{{10\sqrt 3 }}{3}\) cm.
\(\Delta AOH\)vuông tại \(O\), áp dụng định lí Pythagore ta có:
\(A{O^2} = A{H^2} - O{H^2} = 300 - {\left( {\frac{{10\sqrt 3 }}{3}} \right)^2} = 300 - \frac{{300}}{9} = \frac{{800}}{3}\).
Suy ra \(AO = \sqrt {\frac{{800}}{3}} \approx 16,3\) cm.
Đổi \(1{\rm{\;m}} = 100{\rm{\;cm}}\).
Khi đó bạn Nam cần đưa dây diện từ đầu đèn tới trần nhà khoảng là \(100 - 16,3 = 83,7\) cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo