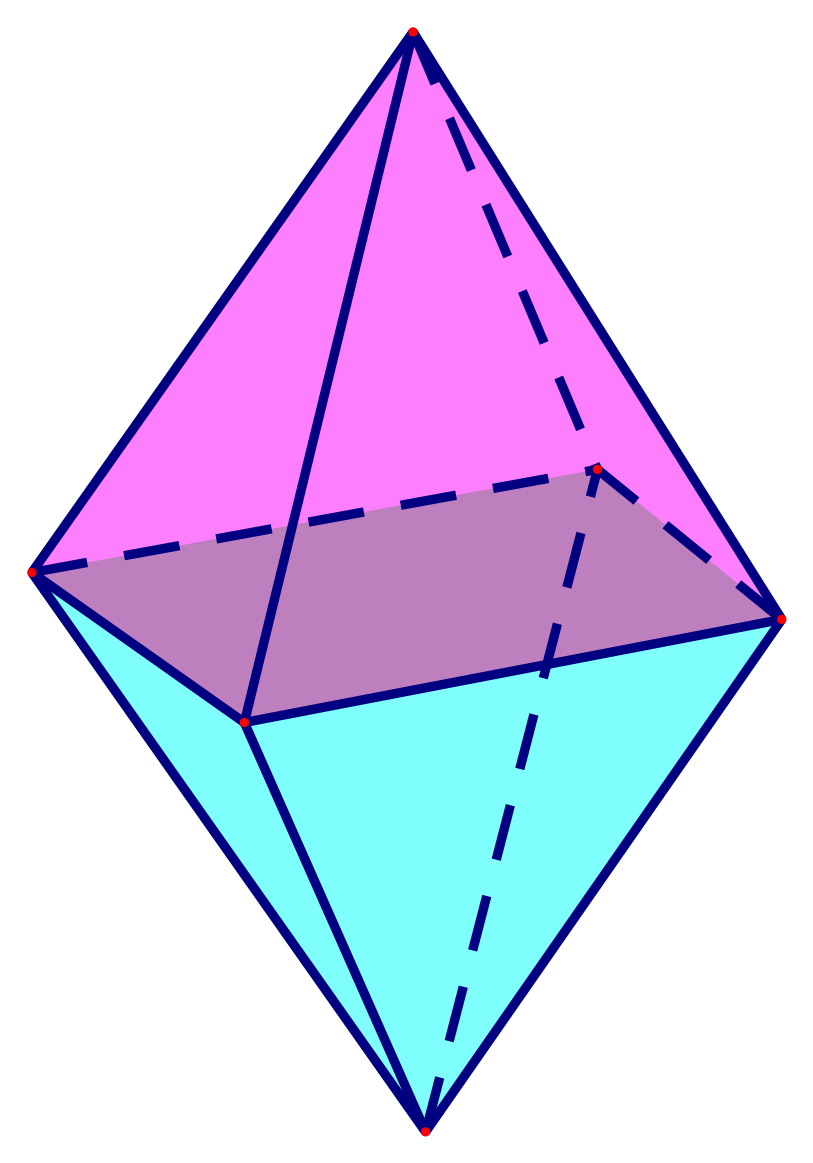
Bạn Như làm một cái lòng đèn hình quả trám (như hình bên) là hình ghép từ hai hình chóp tứ giác đều có cạnh đáy \[20\,\,{\rm{cm}}\], cạnh bên \[32\,\,{\rm{cm}}\,{\rm{,}}\] khoảng cách giữa hai đỉnh của hai hình chóp là \[30\,\,{\rm{cm}}.\]
a) Công thức tính thể tích hình chóp tứ giác đều: \(V = S \cdot h.\)
(Trong đó \(V\) là thể tích, \(S\) là diện tích đáy, \(h\) là chiều cao của hình chóp tứ giác đều).
b) Chiều cao của mỗi hình chóp tứ giác đều là 15 cm.
c) Thể tích của lồng đèn là \(4\,\,000\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}.\)
d) Bạn Như muốn làm 50 cái lòng đèn hình quả trám này cần phải chuẩn bị 165 mét thanh tre? (mối nối giữa các que tre có độ dài không đáng kể).
Bạn Như làm một cái lòng đèn hình quả trám (như hình bên) là hình ghép từ hai hình chóp tứ giác đều có cạnh đáy \[20\,\,{\rm{cm}}\], cạnh bên \[32\,\,{\rm{cm}}\,{\rm{,}}\] khoảng cách giữa hai đỉnh của hai hình chóp là \[30\,\,{\rm{cm}}.\]

a) Công thức tính thể tích hình chóp tứ giác đều: \(V = S \cdot h.\)
(Trong đó \(V\) là thể tích, \(S\) là diện tích đáy, \(h\) là chiều cao của hình chóp tứ giác đều).b) Chiều cao của mỗi hình chóp tứ giác đều là 15 cm.
c) Thể tích của lồng đèn là \(4\,\,000\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}.\)
d) Bạn Như muốn làm 50 cái lòng đèn hình quả trám này cần phải chuẩn bị 165 mét thanh tre? (mối nối giữa các que tre có độ dài không đáng kể).
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án: a) Sai. b) Đúng. c) Đúng. d) Sai.
⦁ a) Công thức tính thể tích hình chóp tứ giác đều: \(V = \frac{1}{3} \cdot S \cdot h.\)
Trong đó \(V\) là thể tích, \(S\) là diện tích đáy, \(h\) là chiều cao của hình chóp tứ giác đều). Do đó ý a) sai.
⦁ Chiều cao của mỗi hình chóp tứ giác đều là: \[30:2 = 15{\rm{ (cm)}}.\]Do đó ý b) đúng.
⦁ Thể tích của lòng đèn quả trám là: \(V = 2 \cdot \left( {\frac{1}{3} \cdot 20 \cdot 20 \cdot 15} \right) = 4\,\,000\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\). Do đó ý c) đúng.
⦁ Bạn Như muốn làm 50 cái lòng đèn hình quả trám này cần phải chuẩn bị số mét thanh tre là:
\[50 \cdot \,\left( {20 \cdot 4 + 32 \cdot 8} \right) = 16\,\,800 (cm) = 168\,\,(m)\].
Vậy bạn Như muốn làm 50 cái lòng đèn hình quả trám này cần phải chuẩn bị 168 mét thanh tre.
Do đó ý d) sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án: \(6\).
Với \(x \ne 3\,;\,\,x \ne - 3\), ta có:
\(B = \left( {\frac{{2x - 1}}{{x + 3}} - \frac{x}{{3 - x}} - \frac{{3 - 10x}}{{{x^2} - 9}}} \right):\frac{{x + 2}}{{x - 3}}\)
\( = \left[ {\frac{{\left( {2x - 1} \right)\left( {x - 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} + \frac{{x\left( {x + 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} - \frac{{3 - 10x}}{{\left( {x + 3} \right)\left( {x - 3} \right)}}} \right] \cdot \frac{{x - 3}}{{x + 2}}\)
\( = \frac{{2{x^2} - 7x + 3 + {x^2} + 3x - 3 + 10x}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\)
\( = \frac{{3{x^2} + 6x}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\)
\( = \frac{{3x\left( {x + 2} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}} = \frac{{3x}}{{x + 3}}\).
Ta có: \(B = \frac{{3x}}{{x + 3}} = \frac{{3x + 9 - 9}}{{x + 3}} = \frac{{3\left( {x + 3} \right)}}{{x + 3}} - \frac{9}{{x + 3}} = 3 - \frac{9}{{x + 3}}\).
Để \(B\) nguyên thì \(\frac{9}{{x + 3}}\) nhận giá trị nguyên.
Suy ra \(x + 3\) là ước của \(9\).
Mà Ư\(\left( 9 \right) = \left\{ { - 9\,;\,\, - 3\,;\,\, - 1\,;\,\,1\,;\,\,3\,;\,\,9} \right\}\).
Ta có bảng sau:
|
\(x + 3\) |
\( - 9\) |
\( - 3\) |
\( - 1\) |
\(1\) |
\(3\) |
\(9\) |
|
\(x\) |
\( - 12\) (TM) |
\( - 6\) (TM) |
\( - 4\) (TM) |
\( - 2\) (TM) |
\(0\) (TM) |
\(6\) (TM) |
Nhận thấy các giá trị \(x\) tìm được đều thỏa mãn.
Do đó, có 6 giá trị nguyên của \(x\) thỏa mãn yêu cầu bài toán.
Lời giải
Hướng dẫn giải
Đáp án: \(52\).
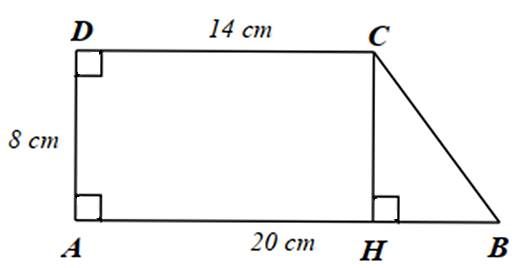
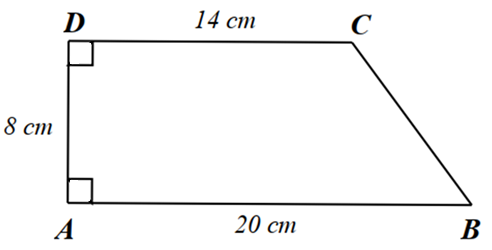
Từ \(C\) kẻ \(CH \bot AB\) tại \(H\).
Xét tứ giác \(ADCH\) có \(\widehat {ADC} = \widehat {DAH} = \widehat {AHC} = 90^\circ \) nên \(ADCH\) là hình chữ nhật.
Suy ra \(AD = CH = 8{\rm{ cm}}\); \(DC = AH = 14{\rm{ cm}}\).
Lại có, \(AH + HB = AB\), suy ra \(BH = AB - AH = 20 - 14 = 6{\rm{ }}\left( {{\rm{cm}}} \right)\).
Áp dụng định lí Pythagore vào tam giác \(\Delta HCB\), có:
\(B{C^2} = H{B^2} + H{C^2} = \)\({8^2} + {6^2} = 100\) suy ra \(BC = 10{\rm{ cm}}\).
Vậy chu vi tứ giác \(ABCD\) là \(8 + 14 + 10 + 20 = 52{\rm{ cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.