Tứ giác \(ABCD\) có \(\widehat C = 50^\circ ,\,\,\widehat D = 60^\circ ,\,\,\widehat A:\widehat B = 3:2.\) Tính \(2\widehat A - \widehat B\) (đơn vị: độ).
Tứ giác \(ABCD\) có \(\widehat C = 50^\circ ,\,\,\widehat D = 60^\circ ,\,\,\widehat A:\widehat B = 3:2.\) Tính \(2\widehat A - \widehat B\) (đơn vị: độ).
Quảng cáo
Trả lời:
Hướng dẫn giải
Tứ giác \(ABCD\) có \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \).
Suy ra \[\widehat A + \widehat B = 360^\circ - \widehat C - \widehat D = 360^\circ - 50^\circ - 60^\circ = 250^\circ .\]
Ta có \(\widehat A:\widehat B = 3:2\) nên \[\frac{{\widehat A}}{{\widehat B}} = \frac{3}{2}\] hay \[\frac{{\widehat A}}{3} = \frac{{\widehat B}}{2}\].
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\[\frac{{\widehat A}}{3} = \frac{{\widehat B}}{2} = \frac{{\widehat A + \widehat B}}{{3 + 2}} = \frac{{250^\circ }}{5} = 50^\circ .\]
Suy ra \[\widehat A = 3 \cdot 50^\circ = 150^\circ \,;\,\,\widehat B = 2 \cdot 50^\circ = 100^\circ .\]
Do đó \(2\widehat A - \widehat B = 2 \cdot 150^\circ - 100^\circ = 200^\circ .\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án: \(6\).
Với \(x \ne 3\,;\,\,x \ne - 3\), ta có:
\(B = \left( {\frac{{2x - 1}}{{x + 3}} - \frac{x}{{3 - x}} - \frac{{3 - 10x}}{{{x^2} - 9}}} \right):\frac{{x + 2}}{{x - 3}}\)
\( = \left[ {\frac{{\left( {2x - 1} \right)\left( {x - 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} + \frac{{x\left( {x + 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} - \frac{{3 - 10x}}{{\left( {x + 3} \right)\left( {x - 3} \right)}}} \right] \cdot \frac{{x - 3}}{{x + 2}}\)
\( = \frac{{2{x^2} - 7x + 3 + {x^2} + 3x - 3 + 10x}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\)
\( = \frac{{3{x^2} + 6x}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\)
\( = \frac{{3x\left( {x + 2} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}} = \frac{{3x}}{{x + 3}}\).
Ta có: \(B = \frac{{3x}}{{x + 3}} = \frac{{3x + 9 - 9}}{{x + 3}} = \frac{{3\left( {x + 3} \right)}}{{x + 3}} - \frac{9}{{x + 3}} = 3 - \frac{9}{{x + 3}}\).
Để \(B\) nguyên thì \(\frac{9}{{x + 3}}\) nhận giá trị nguyên.
Suy ra \(x + 3\) là ước của \(9\).
Mà Ư\(\left( 9 \right) = \left\{ { - 9\,;\,\, - 3\,;\,\, - 1\,;\,\,1\,;\,\,3\,;\,\,9} \right\}\).
Ta có bảng sau:
|
\(x + 3\) |
\( - 9\) |
\( - 3\) |
\( - 1\) |
\(1\) |
\(3\) |
\(9\) |
|
\(x\) |
\( - 12\) (TM) |
\( - 6\) (TM) |
\( - 4\) (TM) |
\( - 2\) (TM) |
\(0\) (TM) |
\(6\) (TM) |
Nhận thấy các giá trị \(x\) tìm được đều thỏa mãn.
Do đó, có 6 giá trị nguyên của \(x\) thỏa mãn yêu cầu bài toán.
Lời giải
Hướng dẫn giải
Đáp án: \(52\).
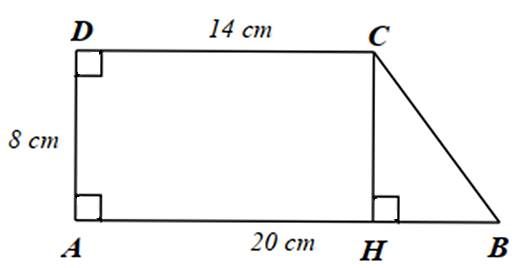
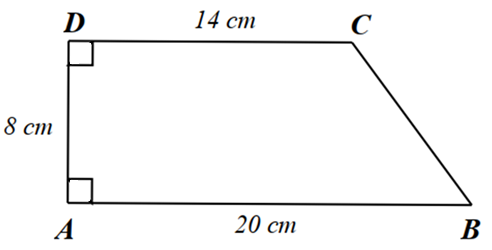
Từ \(C\) kẻ \(CH \bot AB\) tại \(H\).
Xét tứ giác \(ADCH\) có \(\widehat {ADC} = \widehat {DAH} = \widehat {AHC} = 90^\circ \) nên \(ADCH\) là hình chữ nhật.
Suy ra \(AD = CH = 8{\rm{ cm}}\); \(DC = AH = 14{\rm{ cm}}\).
Lại có, \(AH + HB = AB\), suy ra \(BH = AB - AH = 20 - 14 = 6{\rm{ }}\left( {{\rm{cm}}} \right)\).
Áp dụng định lí Pythagore vào tam giác \(\Delta HCB\), có:
\(B{C^2} = H{B^2} + H{C^2} = \)\({8^2} + {6^2} = 100\) suy ra \(BC = 10{\rm{ cm}}\).
Vậy chu vi tứ giác \(ABCD\) là \(8 + 14 + 10 + 20 = 52{\rm{ cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.