Cho góc bẹt \(\widehat {xOy}\). Vẽ tia \(Oz\) sao cho \(\widehat {xOz} = 70^\circ \). Trên nửa mặt phẳng bờ \(Ox\) chứa tia \(Ot\) sao cho \(\widehat {xOt} = 140^\circ \). Vẽ tia \(Om\) là tia đối của tia \(Oz\), tia \(On\) là tia đối của tia \(Ot\).
a) \(\widehat {zOy} = 110^\circ \).
b) \(Oz\) là tia phân giác của \(\widehat {xOy}\).
c) \(\widehat {mOn} = 70^\circ \).
d) \(\widehat {mOy} > \widehat {xOn}.\)
Cho góc bẹt \(\widehat {xOy}\). Vẽ tia \(Oz\) sao cho \(\widehat {xOz} = 70^\circ \). Trên nửa mặt phẳng bờ \(Ox\) chứa tia \(Ot\) sao cho \(\widehat {xOt} = 140^\circ \). Vẽ tia \(Om\) là tia đối của tia \(Oz\), tia \(On\) là tia đối của tia \(Ot\).

a) \(\widehat {zOy} = 110^\circ \).
b) \(Oz\) là tia phân giác của \(\widehat {xOy}\).
c) \(\widehat {mOn} = 70^\circ \).
d) \(\widehat {mOy} > \widehat {xOn}.\)
Quảng cáo
Trả lời:
Đáp án đúng là: a) Đúng b) Sai c) Đúng d) Đúng
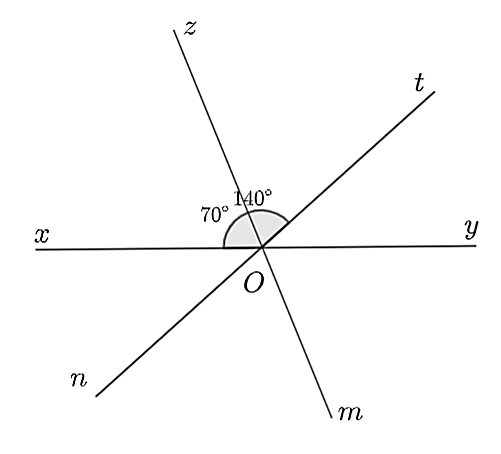
Quan sát hình vẽ, nhận thấy:
• \(\widehat {zOy}\) và \(\widehat {zOx}\) là hai góc kề bù. Do đó, \(\widehat {zOy} + \widehat {zOx} = 180^\circ \) nên \(\widehat {zOy} = 180^\circ - \widehat {zOx} = 180^\circ - 70^\circ = 110^\circ .\)
Do đó, ý a) là đúng.
• Ta có \(Oz\) là tia nằm giữa hai tia \(Ox,Ot\). Lại có, \(\widehat {xOz} = \frac{1}{2}\widehat {xOt}\).
Do đó, \(Oz\) là tia phân giác của \(\widehat {xOt}\). Do đó, ý b) là sai.
• Vì \(Oz\) là tia phân giác của \(\widehat {xOt}\) nên \(\widehat {xOz} = \widehat {zOt} = \frac{1}{2}\widehat {xOt}\).
Do đó, \(\widehat {tOz} = \frac{1}{2} \cdot 140^\circ = 70^\circ \).
Mà \(\widehat {mOn} = \widehat {tOz} = 70^\circ \) (đối đỉnh) .
Do đó, ý c) là đúng.
• Ta có \(\widehat {tOy}\) và \(\widehat {tOx}\) là hai góc kề bù nên \(\widehat {tOy} + \widehat {tOx} = 180^\circ \)
do đó, \(\widehat {tOy} = 180^\circ - \widehat {tOx} = 180^\circ - 140^\circ = 40^\circ .\)
Mà \(\widehat {tOy} = \widehat {xOn} = 40^\circ \) (đối đỉnh) và \(\widehat {xOt} = \widehat {mOy} = 70^\circ \) (đối đỉnh)
Do đó, \(\widehat {mOy} > \widehat {xOn}.\) Do đó, ý d) là đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: a) Sai b) Đúng c) Sai d) Đúng
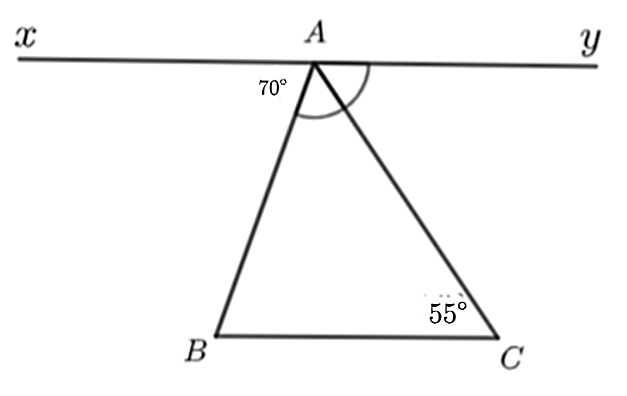
a) Nhận thấy \(\widehat {xAB}\) và \(\widehat {CAB}\) chỉ là hai góc kề nhau do \(\widehat {xAB} + \widehat {CAB} \ne 180^\circ \). Do đó, ý a) sai.
b) Vì tia \(AC\) là tia phân giác của \(\widehat {yAB}\) nên ta có \(\widehat {yAB} = 2\widehat {BAC}\). Do đó, ý b) là đúng.
c) Có \(\widehat {xAB}\) và \(\widehat {yAB}\) là hai góc kề là hai góc kề bù nên ta có \(\widehat {xAB} + \widehat {yAB} = 180^\circ \).
Do đó, \(\widehat {yAB} = 180^\circ - \widehat {xAB} = 180^\circ - 70^\circ = 110^\circ \).
Mà tia \(AC\) là tia phân giác của \(\widehat {yAB}\) nên \(\widehat {yAC} = \widehat {CAB} = \frac{{\widehat {yAB}}}{2} = \frac{{110^\circ }}{2} = 55^\circ \).
Vậy ý c) sai.
d) Ta có: \(\widehat {yAC} = 55^\circ \); \(\widehat {ACB} = 55^\circ \) nên \(\widehat {ACB} = \widehat {yAC}\).
Mà hai góc ở vị trí so le trong nên \(xy\parallel BC\).
Do đó, ý d) đúng.
Lời giải
Đáp án đúng là: a) Đúng b) Sai c) Đúng d) Sai
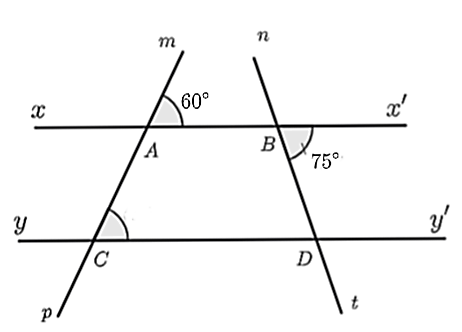
• Nhận thấy \(\widehat {ABD}\) và \(\widehat {DBx'}\) là hai góc kề bù. Do đó, ý a) là đúng.
• Ta có \(\widehat {ABD} + \widehat {DBx'} = 180^\circ \) hay \(\widehat {ABD} + 75^\circ = 180^\circ \) nên \(\widehat {ABD} = 180^\circ - 75^\circ = 105^\circ \). Do đó, ý b) là sai.
• Ta có: \(\widehat {mAB} = \widehat {ACB} = 60^\circ \) (giả thiết)
Mà hai góc ở vị trí đồng vị nên \(xx'\parallel yy'\). Do đó, ý c) là đúng.
• Vì \(xx'\parallel yy'\) nên \(\widehat {CDt} = \widehat {ABD} = 105^\circ \) (hai góc đồng vị). Do đó, ý d) là sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.