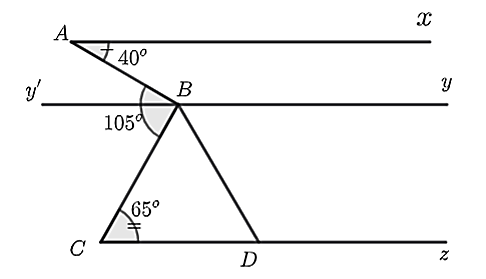
Cho hình vẽ dưới đây, biết rằng \(Ax\parallel yy'\), \(\widehat {xAB} = 40^\circ ,{\rm{ }}\widehat {CBA} = 65^\circ ,{\rm{ }}\widehat {BCy} = 65^\circ \). Kẻ \(BD\) là tia phân giác của \(\widehat {CBy}\).

        a) \(\widehat {ABy'}\) và \(\widehat {y'BC}\) là hai góc kề nhau.

        b) \(\widehat {xAB} = \widehat {BAy'} = 40^\circ \).

        c) \(yy'\parallel Cx.\)

        d) \(\widehat {CDB} > 60^\circ \).

Hướng dẫn giải

Đáp án đúng là: a) Đ                     b) Đ                  c) Đ                                                            d) S

Nhận thấy,

• \(\widehat {ABy'}\) và \(\widehat {y'BC}\) là hai góc kề nhau. Do đó, ý a) đúng.

• Vì \(Ax\parallel yy'\) nên \(\widehat {xAB} = \widehat {BAy'} = 40^\circ \) (so le trong). Do đó, ý b) đúng.

• Lại có \(\widehat {ABy'} + \widehat {y'BC} = \widehat {ABC}\) suy ra \(\widehat {y'BC} = \widehat {ABC} - \widehat {ABy'} = 105^\circ - 40^\circ = 65^\circ \).

Suy ra \(\widehat {CBy'} = \widehat {BCz} = 65^\circ \).

Mà hai góc ở vị trí so le trong nên \(yy'\parallel Cx.\) Do đó, ý c) đúng.

• Có \(\widehat {CBy'}\) và \(\widehat {CBy}\) là hai góc kề bù nên \(\widehat {CBy'} + \widehat {CBy} = 180^\circ \), suy ra \(\widehat {CBy} = 180^\circ - \widehat {CBy'} = 115^\circ \).

Lại có \(BD\) là tia phân giác của \(\widehat {CBy}\) nên \(\widehat {CBD} = \widehat {DBy} = \widehat {\frac{{CBy}}{2}} = \frac{{115^\circ }}{2} = 57,5^\circ \).

Vì \(yy'\parallel Cx\) nên \(\widehat {CBy} = \widehat {CDB} = 57,5^\circ \) (so le trong)

Do đó, \(\widehat {CDB} < 60^\circ \).

Vậy ý d) là sai.