Dữ liệu Câu 3 - 4: Hai điện tích điểm q1 = - 10-9 C và q2 = 10-9 C đặt tại hai điểm A, B cách nhau 40 cm trong chân không.
Cường độ điện trường tổng hợp tại M cách A 20 cm và cách B 60cm có độ lớn là bao nhiêu? (tính theo V/m)
Dữ liệu Câu 3 - 4: Hai điện tích điểm q1 = - 10-9 C và q2 = 10-9 C đặt tại hai điểm A, B cách nhau 40 cm trong chân không.
Quảng cáo
Trả lời:
\({E_1} = \frac{{k\left| q \right|}}{{\varepsilon {{(r)}^2}}} = \frac{{{{9.10}^9}\left| { - {{6.10}^{ - 9}}} \right|}}{{1.{{(0,2)}^2}}} = 1350(V/m)\)
\({E_2} = \frac{{k\left| {{q_2}} \right|}}{{\varepsilon {{(r)}^2}}} = \frac{{{{9.10}^9}\left| {{{6.10}^{ - 9}}} \right|}}{{1.{{(0,6)}^2}}} = 150(V/m)\)
Áp dụng nguyên lý chồng chất điện trường:
\({\overrightarrow E _1} \uparrow \downarrow {\overrightarrow E _2} \Leftrightarrow {E_M} = \left| {{E_1} - {E_2}} \right| = \left| {1350 - 150} \right| = 1200(V/m)\)
Câu hỏi cùng đoạn
Câu 2:
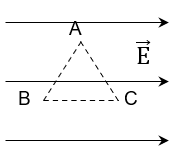
Điểm N nằm trên đoạn AB và cách đều AB. Tìm độ lớn cường độ điện trường tại N. (tính theo V/m)
Điểm N nằm trên đoạn AB và cách đều AB. Tìm độ lớn cường độ điện trường tại N. (tính theo V/m)
\({E_1} = {E_2} = \frac{{k\left| q \right|}}{{\varepsilon {{(r)}^2}}} = \frac{{{{9.10}^9}\left| { - {{6.10}^{ - 9}}} \right|}}{{1.{{(0,2)}^2}}} = 1350(V/m)\)
Áp dụng nguyên lý chồng chất điện trường:
\({\overrightarrow E _1} \uparrow \uparrow {\overrightarrow E _2} \Leftrightarrow {E_N} = {E_1} + {E_2} = 1350 + 1350 = 2700(V/m)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
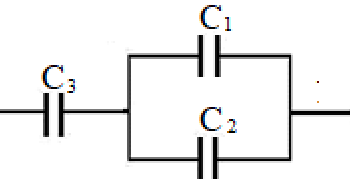
Câu 1
Lời giải
\(\left[ {{C_3}{\rm{ }}nt{\rm{ }}\left( {{C_1}{\rm{//}}{{\rm{C}}_2}} \right)} \right]\)
\({C_b} = \frac{{{C_3}{C_{12}}}}{{{C_3} + {C_{12}}}} = \frac{{20.5}}{{20 + 5}} = 4\mu C\)
\(Q = {C_b}U = 4.30 = 120nC\)
Lời giải
Chọn B
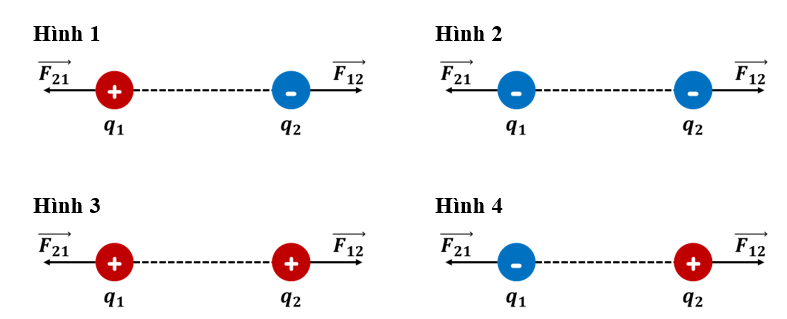
Hình 1 và hình 4 không chính xác. Tương tác giữa hai điện tích trái dấu là hút nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.