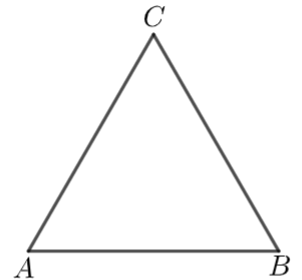
Cho tam giác \(ABC\)đều và có \(BC = 7\;{\rm{cm}}\)như hình vẽ dưới đây:
Khi đó:
(a)Các cạnh của tam giác \(ABC\) là \(AB,\,\,AC,\,\,BC\).
(b)\(AB = 7\,{\rm{cm}}{\rm{.}}\)
(c)Góc \(A = \)góc \(B = \) góc \(C = 60^\circ \).
(d)Tổng ba cạnh của tam giác \(ABC\) bằng \(28{\rm{ cm}}{\rm{.}}\)
Quảng cáo
Trả lời:
a) Đúng.
Các cạnh của tam giác \(ABC\) là \(AB,\,\,AC,\,\,BC\).
b) Đúng.
Vì tam giác \(ABC\) là tam giác đều nên \(AB = BC = AC = 7{\rm{ cm}}{\rm{.}}\)
c) Đúng.
Tam giác \(ABC\) là tam giác đều nên góc \(A = \)góc \(B = \) góc \(C = 60^\circ \).
d) Sai.
Vì tam giác \(ABC\) đều nên \(AB = BC = AC = 7{\rm{ cm}}{\rm{.}}\)
Do đó, tổng ba cạnh của tam giác \(ABC\) bằng \(7 + 7 + 7 = 21{\rm{ }}\left( {{\rm{cm}}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: C
A, B, D đúng.
Câu c) sai vì: Sáu góc trong hình lục giác đều bằng nhau, mỗi góc bằng \(120^\circ .\)
Lời giải
Đáp án đúng là: A
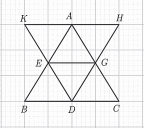
Hình gợi lên hình lục giác đều là Hình 1.

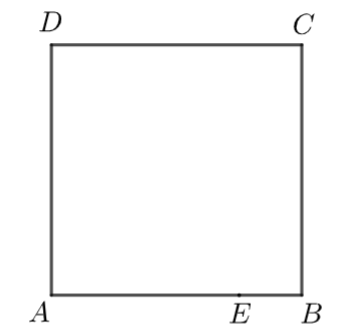
Vì \(ABCD\) là hình vuông nên \(AB < AC,\;\,AB = BC,\,\;AB = AD,\;\,AB = CD.\) Do đó, chọn đáp án A.
Câu 3
\(AB.\)
\(AD.\)
\(AC.\)
\(AE.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\(3\;{\rm{cm}}{\rm{.}}\)
\(4\;{\rm{cm}}{\rm{.}}\)
\(5\;{\rm{cm}}{\rm{.}}\)
\(6\;{\rm{cm}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\(60^\circ .\)
\(90^\circ .\)
\(100^\circ .\)
\(120^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.