Nhà bạn thu có một đèn trang trí có dạng hình chóp tam giác đều như hình bẽ bên. Các cạnh của hình chóp đều bằng nhau và bằng \(20{\rm{ cm}}\). Bạn Thu dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu.
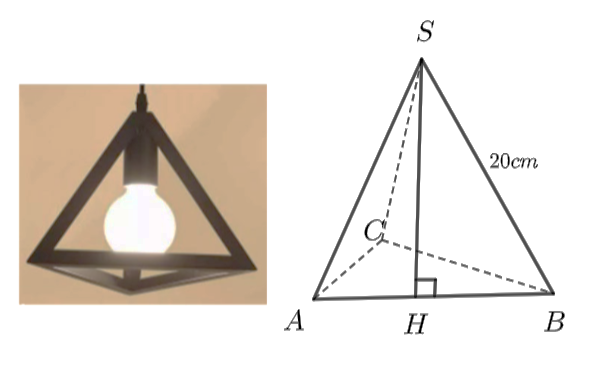
Tính diện tích giấy màu mà bạn Thu sử dụng (đơn vị: cm2, coi như mép dán không đáng kể). Cho biết \(\sqrt {300} = 17,32\). (Kết quả làm tròn đến hàng đơn vị)
Nhà bạn thu có một đèn trang trí có dạng hình chóp tam giác đều như hình bẽ bên. Các cạnh của hình chóp đều bằng nhau và bằng \(20{\rm{ cm}}\). Bạn Thu dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu.

Tính diện tích giấy màu mà bạn Thu sử dụng (đơn vị: cm2, coi như mép dán không đáng kể). Cho biết \(\sqrt {300} = 17,32\). (Kết quả làm tròn đến hàng đơn vị)
Quảng cáo
Trả lời:
Đáp án: 520
Các mặt bên và mặt đáy của hình chóp \(S.ABC\) là những tam giác đều cạnh \(20{\rm{ cm}}{\rm{.}}\)
Xét tam giác đều \(SAB\) có đường cao \(SH\) đồng thời là đường trung tuyến, ta có:
\(AH = BH = \frac{{AB}}{2} = 10{\rm{ cm}}\).
Xét tam giác \(SHB\) vuông tại \(H\). Theo định lí Pythagore, ta có:
\(S{B^2} = S{H^2} + B{H^2}\) hay \({20^2} = S{H^2} + {10^2}\) suy ra \(S{H^2} = S{B^2} - B{H^2} = 300\).
Suy ra \(SH = \sqrt {300} \approx 17,32{\rm{ }}\left( {{\rm{cm}}} \right)\).
Diện tích xung quanh của hình chóp tam giác đều \(S.ABC\) là:
\({S_{xq}} = 3 \cdot \frac{1}{2} \cdot 30 \cdot 17,32 = 519,6 \approx 520{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng.
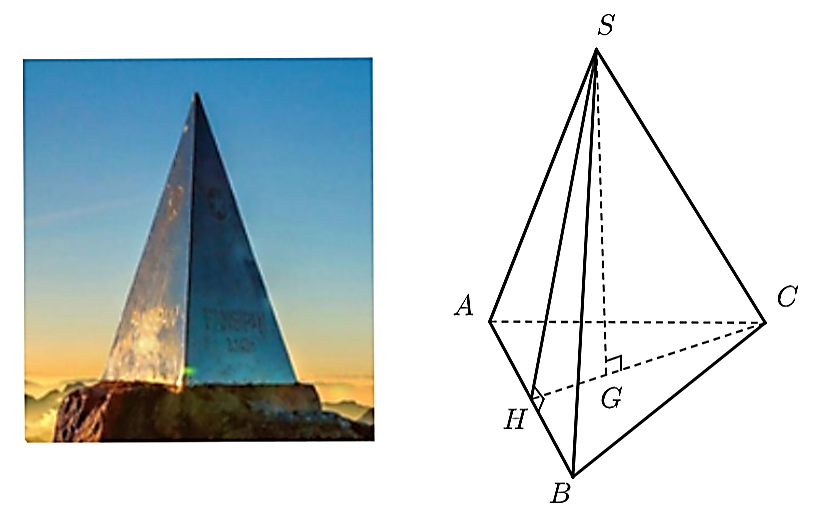
Mặt đáy của hình chóp \(S.ABC\) là một tam giác đều \(ABC\) có cạnh \(60{\rm{ cm}}{\rm{.}}\) Gọi đường cao của mặt đáy là \(CH\), ta có \(CH\) đồng thời là đường trung tuyến.
\(HA = HB = \frac{{AB}}{2} = 30{\rm{ cm}}{\rm{.}}\)
b) Đúng.
Xét tam giác \(BHC\) vuông tại \(H\). Theo định lý Pythagore ta có: \(C{B^2} = H{B^2} + H{C^2}\) hay \({60^2} = {30^2} + H{C^2}\) suy ra \(C{H^2} = {60^2} - {30^2} = 2{\rm{ }}700\) nên \(CH = \sqrt {2700} = 30\sqrt 3 {\rm{ }}\left( {{\rm{cm}}} \right)\).
c) Sai.
Vì \(G\) là trọng tâm của mặt đáy nên \(GH = \frac{1}{3}HC = \frac{{30\sqrt 3 }}{3} = 10\sqrt 3 {\rm{ }}\left( {{\rm{cm}}} \right)\).
Hình chóp \(S.ABC\) có đường cao \(SG\) nên \(SG \bot HC.\)
Xét tam giác \(SHG\) vuông tại \(G\). Theo định lý Pythagore, ta có:
\(S{H^2} = S{G^2} + H{G^2}\)
\(S{H^2} = {90^2} + {30^2} = 9000\)
Suy ra \(SH = \sqrt {9000} = 30\sqrt {10} {\rm{ cm}}{\rm{.}}\)
d) Đúng.
Vậy diện tích xung quanh của hình chóp là \(S = 3 \cdot \frac{1}{2} \cdot 60 \cdot 30\sqrt {10} \approx 8538{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Lời giải
Đáp án: 1836
Ta minh họa bảo tàng bằng hình chóp tứ giác sau:
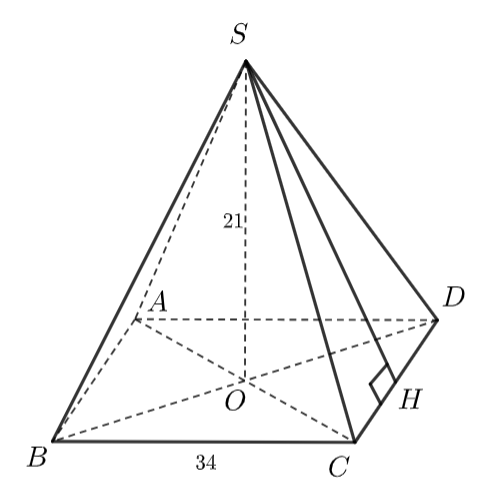
Đường cao của hình chóp \(SO\) vuông góc với mặt đáy \(ABCD\) nên \(SO \bot OH.\)
Dễ thấy \(OH = \frac{1}{2}DC = \frac{1}{2}.34 = 17{\rm{ }}\left( {\rm{m}} \right)\)
Xét tam giác \(SOH\) vuông tại \(O.\)
Theo định lí Pythagore, ta có: \(S{H^2} = S{O^2} + O{H^2}\)
Suy ra \(S{H^2} = {21^2} + {17^2} = 730\)
Suy ra \(SH = \sqrt {730} \approx 27{\rm{ }}\left( {\rm{m}} \right)\).
Nửa chu vi mặt đáy là: \(P = \frac{1}{2}\left( {34 + 34 + 34 + 34} \right) = 68{\rm{ }}\left( {\rm{m}} \right)\)
Tổng diện tích các tấm kính để phủ kín bốn mặt bên của bảo tàng hình chóp này là:
\({S_{xq}} = 68.27 = 1836{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.