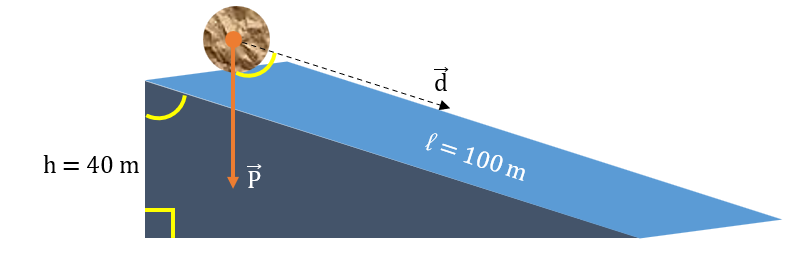
Một vật có khối lượng \(500{\rm{\;g}}\) nằm trên đỉnh của một mặt phẳng nghiêng có chiều dài \(14{\rm{\;m}}\), nghiêng góc \({30^ \circ }\) so với mặt phẳng ngang. Lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\), chọn mốc tính thế năng tại chân mặt phẳng nghiêng và bỏ qua lực cản của môi trường. Thế năng trọng trường của vật là
\(35{\rm{\;J}}\).
\(70{\rm{\;J}}\).
\(50{\rm{\;J}}\).
\(100{\rm{\;J}}\).
Câu hỏi trong đề: Bài tập ôn tập Vật lí 10 Cánh diều Chủ đề 3 có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng: A
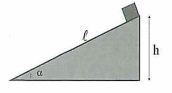
Mốc thế năng tại mặt đất, độ cao của vật so với mốc thế năng là:
\({\rm{h}} = \ell {\rm{sin}}\alpha = 14 \cdot {\rm{sin}}{30^ \circ } = 7{\rm{\;m}}\).
Thế năng trọng trường của vật là: \({{\rm{W}}_{\rm{t}}} = {\rm{m}}{\rm{.g}}{\rm{.h}} = 0,5.10.7 = 35{\rm{\;J}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
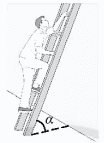
Ta có: \(\cos \alpha = \frac{l}{d} = \frac{{1,375}}{{2,75}}\) \(\alpha = 60^\circ \).
Công của trọng lực tác dụng lên kĩ sư khi người này leo từ chân đến đỉnh thang:
\({A_P} = P.d.\cos \left( {\vec P;\vec d} \right) = m.g.d.\cos \left( {\vec P;\vec d} \right) = 65.10.2,75.\cos \left( {90^\circ + 60^\circ } \right) \approx - 1,5\) kJ.
Câu 2
có thể dương hoặc bằng không.
Phụ thuộc vào hệ quy chiếu.
tỉ lệ với khối lượng của vật.
tỉ lệ với vận tốc của vật.
Lời giải
Đáp án đúng: D
\({W_d} = \frac{1}{2}m{v^2}\)nên động năng của một vật tỉ lệ với bình phương tốc độ của vật.
Câu 3
24 \(\sqrt 3 \) kJ.
36 \(\sqrt 3 \) kJ.
\(12\sqrt 3 \)kJ.
36 kJ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
vật rơi trong không khí.
vật trượt có ma sát.
vật rơi tự do.
vật rơi trong chất lỏng nhớt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
48 000 J.
4 800 J.
\(60\sqrt 3 \) kJ.
60 kJ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.