Một viên đạn khối lượng \(10{\rm{\;g}}\) đang bay với tốc độ \(600{\rm{\;m}}/{\rm{s}}\) thì gặp một bức tường. Đạn xuyên qua tường trong thời gian \(0,01{\rm{\;s}}\). Sau khi xuyên qua tường, tốc độ của đạn còn \(200{\rm{\;m}}/{\rm{s}}\). Lực cản của tường tác dụng lên viên đạn
ngược hướng chuyển động của viên đạn và có độ lớn \(400{\rm{\;N}}\).
cùng hướng chuyển động của viên đạn và có độ lớn \(400{\rm{\;N}}\).
ngược hướng chuyển động của viên đạn và có độ lớn \(800{\rm{\;N}}\).
cùng hướng chuyển động của viên đạn và có độ lớn \(800{\rm{\;N}}\).
Câu hỏi trong đề: Bài tập ôn tập Vật lí 10 Cánh diều Chủ đề 4 có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng: A
Phân tích:
Có thể mô tả chuyển động của viên đạn trước và sau khi xuyên qua tường như sau:
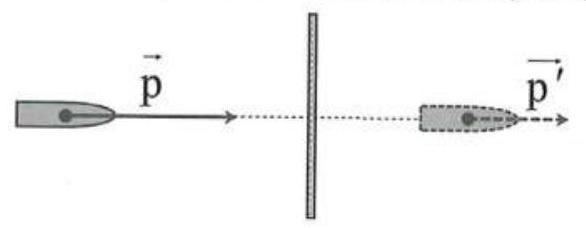
Có thể thấy hướng chuyển động của viên đạn không thay đổi, do đó nếu chọn trục Ox theo hướng chuyển động của viên đạn thì trong biểu thức liên hệ giữa xung lượng của lực và độ biến thiên động lượng ta có thể bỏ dấu vectơ và xác định chiều của các vectơ căn cứ vào dấu của các đại lượng.
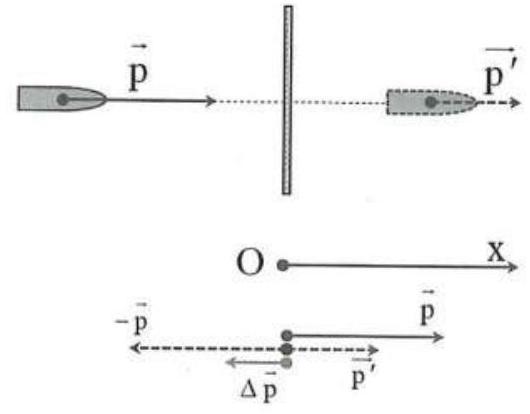
Biểu thức có thể viết như sau: \({{\rm{F}}_{\rm{c}}}{\rm{.\Delta t}} = {\rm{p'}} - {\rm{p}}\).
\({\rm{m}} = 10{\rm{\;g}} = 0,01{\rm{\;kg}}\); Chọn trục \({\rm{Ox}}\) như hình vẽ.
Ta có: \({\rm{v}} = 600{\rm{\;m}}/{\rm{s}};{\rm{v'}} = 200{\rm{\;m}}/{\rm{s}}\).
Động lượng của đạn trước khi gặp tường là:
\({\rm{p}} = {\rm{mv}} = 0,01.600 = 6{\rm{\;kg}}{\rm{.m/s}}\).
Động lượng của đạn sau sau khi xuyên qua tường là:
\({\rm{p'}} = {\rm{mv'}} = 0,01.200 = 2{\rm{\;kg}}{\rm{.m/s}}{\rm{.\;}}\)
Từ mối liên hệ giữa xung lượng của lực và độ biến thiên động lượng ta có:
\({\rm{p'}} - {\rm{p}} = {{\rm{F}}_{\rm{c}}}{\rm{.\Delta t}} \Rightarrow {{\rm{F}}_{\rm{c}}} = \frac{{{\rm{p'}} - {\rm{p}}}}{{{\rm{\Delta t}}}} = \frac{{2 - 6}}{{0,01}} = - 400{\rm{\;N}}\).
Dấu "-" chứng tỏ \({{\rm{\vec F}}_{\rm{c}}}\) ngược hướng chuyển động của viên đạn, và có độ lớn là \(400{\rm{\;N}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đ
b) Đ
c) Khi vật chuyển động trên mặt phẳn nghiêng, trọng lực làm thay đổi động lượng nên không thể là hệ kín => S.
d) Trong chuyển động tròn đều \(\overrightarrow v \) đổi hướng nên \(\overrightarrow p \) không bảo toàn hướng => S.
Câu 2
\(8{\rm{\;N}}\).
\(8\sqrt 3 {\rm{\;N}}\).
\(16{\rm{\;N}}\).
\(16\sqrt 3 {\rm{\;N}}\).
Lời giải
Hướng dẫn giải
Đáp án đúng: B
Có thể mô tả chuyển động của quả bóng trước và sau khi va chạm với tường như sau:
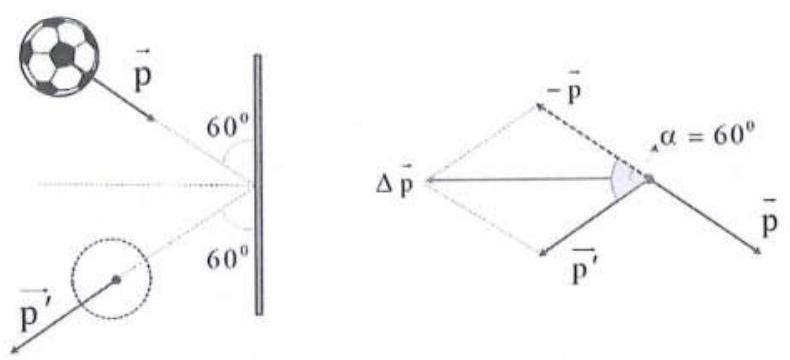
Từ mối liên hệ giữa xung lượng của lực và độ biến thiên động lượng ta xác định được độ lớn của lực tương tác giữa bóng và tường: \({\rm{\Delta \vec p}} = {\rm{\vec F}}{\rm{.\Delta t}} \Rightarrow {\rm{F}} = \frac{{{\rm{\Delta p}}}}{{{\rm{\Delta t}}}}\).
Trong đó .
Tốc độ của bóng trước và sau va chạm bằng nhau nên động lượng có độ lớn như nhau, ta có:
\({\rm{p'}} = {\rm{p}} = {\rm{mv}} = 0,2.\frac{{72}}{{3,6}} = 4{\rm{\;kg}}{\rm{.m/s}}\).
Độ biến thiên động lượng của quả bóng
.
Từ mối liên hệ giữa xung lượng của lực và độ biến thiên động lượng ta có:
\({\rm{\Delta \vec p}} = {\rm{\vec F}}{\rm{.\Delta t}} \Rightarrow {\rm{F}} = \frac{{{\rm{\Delta p}}}}{{{\rm{\Delta t}}}} = \frac{{4\sqrt 3 }}{{0,5}} = 8\sqrt 3 {\rm{\;N}}{\rm{.\;}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
\(10{\rm{\;m/s}}\).
\(5\sqrt {10} {\rm{\;m/s}}\).
\(10\sqrt 5 {\rm{\;m/s}}\).
\(50{\rm{\;m/s}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
độ lớn \(20{\rm{\;kg}}.{\rm{m/s}}\); phương thẳng đứng, chiều từ trên xuống dưới.
độ lớn \(20{\rm{\;kg}}{\rm{.m/s}}\); phương thẳng đứng, chiều từ dưới lên trên.
độ lớn \(20000{\rm{\;kg}}{\rm{.m/s}}\); phương thẳng đứng, chiều từ trên xuống dưới.
độ lớn \(20000{\rm{\;kg}}.{\rm{m/s}}\); phương thẳng đứng, chiều từ dưới lên trên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
\(155{\rm{\;m}}/{\rm{s}}\).
\(255{\rm{\;m}}/{\rm{s}}\).
\(1525{\rm{\;m}}/{\rm{s}}\).
\(1225{\rm{\;m}}/{\rm{s}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.