Một khẩu súng có khối lượng \(4{\rm{\;kg}}\) bắn ra một viên đạn theo phương ngang có khối lượng \(50{\rm{\;g}}\). Khi viên đạn thoát ra khỏi nòng súng thì súng giật lùi với tốc độ \(1,2{\rm{\;m}}/{\rm{s}}\). Tốc độ của đạn khi ra khỏi nòng súng là
\(96{\rm{\;m}}/{\rm{s}}\).
\(94,8{\rm{\;m}}/{\rm{s}}\).
\(94,8{\rm{\;cm}}/{\rm{s}}\).
\(96{\rm{\;cm}}/{\rm{s}}\).
Câu hỏi trong đề: Bài tập ôn tập Vật lí 10 Cánh diều Chủ đề 4 có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng: B
Phân tích:
Xét hệ gồm súng (khối lượng M) và đạn (khối lượng \({\rm{m}}\)). Chuyển động của súng và đạn dựa trên nguyên tắc chuyển động bằng phản lực.
Cần chú ý ở đây trước khi bắn đạn nằm trong súng do đó khối lượng \(4{\rm{\;kg}}\) tương ứng với tổng khối lượng của súng và đạn: \(M + m = 4{\rm{\;kg}}\).
Xét hệ gồm súng (khối lượng \({\rm{M}} = 4 - 0,05 = 3,95{\rm{\;kg}}\) ) và đạn (khối lượng \({\rm{m}} = 0,05{\rm{\;kg}}\)), hệ là kín. Động lượng của hệ trước khi bắn là: \({{\rm{\vec p}}_{\rm{t}}} = \vec 0\).
Động lượng của hệ sau khi bắn súng là: \({{\rm{\vec p}}_{\rm{s}}} = {\rm{M}}{\rm{.\vec V}} + {\rm{m}}{\rm{.\vec v}}\).
Áp dụng định luật bảo toàn động lượng: \(M.\vec V + m.\vec v = \vec 0 \Rightarrow \vec v = - \frac{M}{m}\vec V\).
Tốc độ của đạn khi ra khỏi nòng súng là: \({\rm{v}} = \frac{{\rm{M}}}{{\rm{m}}}{\rm{.V}} = \frac{{3,95}}{{0,05}}.1,2 = 94,8{\rm{\;m}}/{\rm{s}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đ
b) Đ
c) Khi vật chuyển động trên mặt phẳn nghiêng, trọng lực làm thay đổi động lượng nên không thể là hệ kín => S.
d) Trong chuyển động tròn đều \(\overrightarrow v \) đổi hướng nên \(\overrightarrow p \) không bảo toàn hướng => S.
Câu 2
\(8{\rm{\;N}}\).
\(8\sqrt 3 {\rm{\;N}}\).
\(16{\rm{\;N}}\).
\(16\sqrt 3 {\rm{\;N}}\).
Lời giải
Hướng dẫn giải
Đáp án đúng: B
Có thể mô tả chuyển động của quả bóng trước và sau khi va chạm với tường như sau:
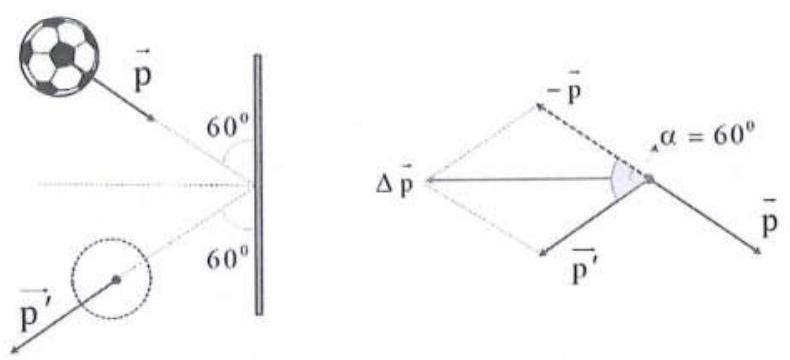
Từ mối liên hệ giữa xung lượng của lực và độ biến thiên động lượng ta xác định được độ lớn của lực tương tác giữa bóng và tường: \({\rm{\Delta \vec p}} = {\rm{\vec F}}{\rm{.\Delta t}} \Rightarrow {\rm{F}} = \frac{{{\rm{\Delta p}}}}{{{\rm{\Delta t}}}}\).
Trong đó .
Tốc độ của bóng trước và sau va chạm bằng nhau nên động lượng có độ lớn như nhau, ta có:
\({\rm{p'}} = {\rm{p}} = {\rm{mv}} = 0,2.\frac{{72}}{{3,6}} = 4{\rm{\;kg}}{\rm{.m/s}}\).
Độ biến thiên động lượng của quả bóng
.
Từ mối liên hệ giữa xung lượng của lực và độ biến thiên động lượng ta có:
\({\rm{\Delta \vec p}} = {\rm{\vec F}}{\rm{.\Delta t}} \Rightarrow {\rm{F}} = \frac{{{\rm{\Delta p}}}}{{{\rm{\Delta t}}}} = \frac{{4\sqrt 3 }}{{0,5}} = 8\sqrt 3 {\rm{\;N}}{\rm{.\;}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
\(10{\rm{\;m/s}}\).
\(5\sqrt {10} {\rm{\;m/s}}\).
\(10\sqrt 5 {\rm{\;m/s}}\).
\(50{\rm{\;m/s}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
độ lớn \(20{\rm{\;kg}}.{\rm{m/s}}\); phương thẳng đứng, chiều từ trên xuống dưới.
độ lớn \(20{\rm{\;kg}}{\rm{.m/s}}\); phương thẳng đứng, chiều từ dưới lên trên.
độ lớn \(20000{\rm{\;kg}}{\rm{.m/s}}\); phương thẳng đứng, chiều từ trên xuống dưới.
độ lớn \(20000{\rm{\;kg}}.{\rm{m/s}}\); phương thẳng đứng, chiều từ dưới lên trên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
\(155{\rm{\;m}}/{\rm{s}}\).
\(255{\rm{\;m}}/{\rm{s}}\).
\(1525{\rm{\;m}}/{\rm{s}}\).
\(1225{\rm{\;m}}/{\rm{s}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.