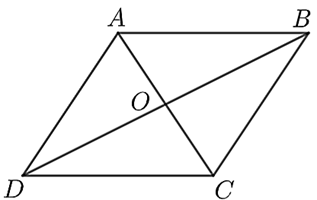
Cho hình bình hành \(ABCD.\) Gọi \(O\) là giao điểm của hai đường chéo và \(OA = 3\;{\rm{cm}}{\rm{.}}\) Khi đó:
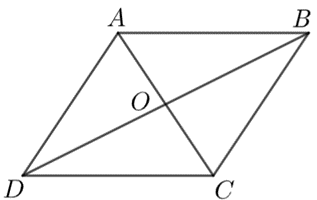
Cho hình bình hành \(ABCD.\) Gọi \(O\) là giao điểm của hai đường chéo và \(OA = 3\;{\rm{cm}}{\rm{.}}\) Khi đó:

Quảng cáo
Trả lời:
Đáp án đúng là: A
Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm mỗi đường.
Vì \(ABCD\) là hình bình hành, \(O\) là giao điểm của hai đường chéo nên \(O\) là trung điểm của \(AC.\)
Do đó, \(OC = OA = 3\;{\rm{cm}}{\rm{.}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 75
Độ dài \(NP\) là: \(45:3 = 15\,\,\left( {{\rm{cm}}} \right)\).
Diện tích hình bình hành \(MNPQ\) là: \(5 \cdot 15 = 75\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Lời giải
a) Đúng.
Tổng độ dài hai cạnh \(AD\) và \(AB\) là: \(58:2 = 29\,\,\left( {{\rm{cm}}} \right)\).
Vì \(AD\) và \(AB\) là hai số tự nhiên liên tiếp, đồng thời nhận thấy \(29 = 14 + 15\).
Ngoài ra, \(AD < BC\).
Do đóm độ dài cạnh \(AD\) và \(AB\) lần lượt là 14 cm và 15 cm.
b) Sai.
Có \(MB\) hơn \(AM\) là 5 cm nên độ dài đoạn \(AM\) là: \(\left( {15 - 5} \right):2 = 5\,\,\left( {{\rm{cm}}} \right)\).
c) Sai.
Chu vi của hình bình hành \(AMND\) là: \(2 \cdot \left( {5 + 14} \right) = 38{\rm{ }}\left( {{\rm{cm}}} \right)\).
d) Sai.
Chu vi hình bình hành \(MBCN\) là: \(2 \cdot \left( {15 - 5 + 14} \right) = 48{\rm{ }}\left( {{\rm{cm}}} \right)\).
Do đó, chu vi hình bình hành \(MBCN\) hơn chu vi hình bình hành \(AMND\) là \(48 - 38 = 10\,\,\left( {{\rm{cm}}} \right)\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.