Cho hình chữ nhật \(ABCD\) có \(AB = 4BC\) và diện tích bằng \(100\,{{\rm{m}}^2}.\) Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(AB,\,AM\) và \(MB\).
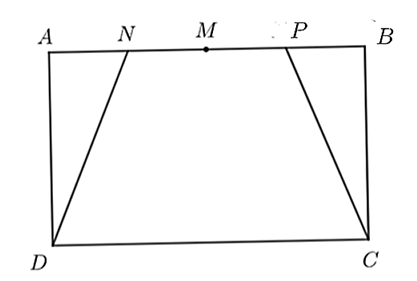
Tính diện tích hình thang cân \(NPCD\). (Đơn vị: m2)
Cho hình chữ nhật \(ABCD\) có \(AB = 4BC\) và diện tích bằng \(100\,{{\rm{m}}^2}.\) Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(AB,\,AM\) và \(MB\).

Tính diện tích hình thang cân \(NPCD\). (Đơn vị: m2)
Quảng cáo
Trả lời:
Đáp án: 75
Có diện tích hình chữ nhật \(ABCD\) là: \(AB \cdot BC = 100\) hay \(4B{C^2} = 100\) nên \(B{C^2} = 25 = {5^2}\).
Do đó, \(BC = 5\,\,\left( {{\rm{cm}}} \right),\,AB = 4BC = 20\,\,\left( {{\rm{cm}}} \right)\).
Theo đề thì \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(AB,\,AM\) và \(MB\).
Nên \(NP = NM + MP = \frac{1}{2}AM + \frac{1}{2}MB = MB = \frac{1}{2}AB = 10{\rm{ cm}}{\rm{.}}\)
Diện tích của hình thang \(NPCD\) là: \(\frac{{\left( {NP + DC} \right) \cdot BC}}{2} = \frac{{\left( {10 + 20} \right) \cdot 5}}{2} = 75{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: A
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Lời giải
Đáp án: 48
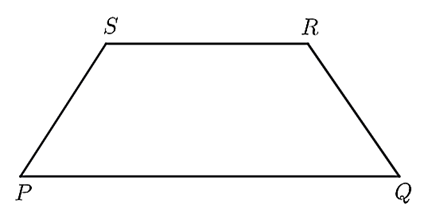
Độ dài đáy \(RS\) là: \(20 - 12 = 8\,\,\left( {{\rm{cm}}} \right)\).
Độ dài cạnh bên là: \(\frac{1}{2} \cdot 20 = 10\,\,\left( {{\rm{cm}}} \right)\).
Chu vi của hình thang cân \(PQRS\) là: \(20 + 8 + 10 + 10 = 48{\rm{ }}\left( {{\rm{cm}}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.