Sau một trận bão lớn, một cái cây mọc thẳng đứng ở vị trí \(C\) đã bị gãy ngang tại \(A\) (như hình vẽ). Ngọn cây chạm mặt đất cách gốc một khoảng \(BC = 5{\rm{ m}}\). Biết rằng phần ngọn bị gãy \(AB\) và phần gốc \(AC\) có tỉ lệ \(3:2\). (Các kết quả làm tròn đến chữ số thập phân thứ hai)

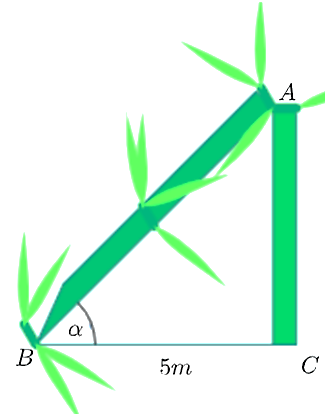
    a) \(\sin \widehat {ABC} = \frac{2}{3}.\)

    b) Góc tạo bởi phần thân bị gãy và mặt đất nhỏ hơn \(42^\circ \).

    c) Độ dài phần ngọn bị gãy nhỏ hơn \(6,5{\rm{ m}}{\rm{.}}\)

    d) Chiều cao ban đầu của cây khoảng \(11,18{\rm{ m}}{\rm{.}}\)

Hướng dẫn giải

a) Vì \(AM,\,\,AN\) là hai tiếp tuyến của đường tròn \(\left( O \right)\) lần lượt tại \(M,\,\,N\) nên \(AM \bot OM,\,\,AN \bot ON.\)

Gọi \[E\] là trung điểm của \[OA\]. Khi đó \(OE = AE = \frac{1}{2}OA.\)

Xét \[\Delta MOA\] vuông tại \[M\] có \[ME\] là đường trung tuyến ứng với cạnh huyền \(OA\) nên \[ME = \frac{1}{2}OA\].

Xét \[\Delta NOA\] vuông tại \[N\] có \[NE\] là đường trung tuyến ứng với cạnh huyền \(OA\) nên \[NE = \frac{1}{2}OA\].

Vì \[NE = ME = OE = AE = \frac{1}{2}OA\] nên bốn điểm \[A,M,O,N\] cùng thuộc đường tròn tâm \[E,\] đường kính \[OA\].

b) Xét \[\Delta COB\] cân tại \[O\] (do \[OC = OB\]) có \[OI\] là đường trung tuyến nên đồng thời là đường cao, do đó \[OI \bot BC\]. Suy ra \[\Delta IOA\] vuông tại \[I\].

Xét \[\Delta IOA\] vuông tại \[I\] có \[IE\] là đường trung tuyến ứng với cạnh huyền \(OA\) nên \[IE = \frac{1}{2}OA\].

Khi đó, ta có \[NE = IE = OE = AE = \frac{1}{2}OA\] nên bốn điểm \[A,I,O,N\] cùng thuộc đường tròn tâm \[E,\] đường kính \[OA\].

Suy ra \[\widehat {AIN} = \widehat {AON}\] (hai góc nội tiếp cùng chắn cung \[AN\] của đường tròn tâm \[E\]). (*)

Xét đường tròn \(\left( O \right)\) có \[AM,AN\] là hai tiếp tuyến cắt nhau tại \[A\], suy ra \[OA\] là phân giác của \[\widehat {MON}\]

Do đó, \[\widehat {AON} = \frac{1}{2}\widehat {MON}\].

Mà \[\widehat {NFM} = \frac{1}{2}\widehat {MON}\] (góc nội tiếp và góc ở tâm cùng chắn cung \[MN\])

Suy ra \[\widehat {NFM} = \widehat {AON}\] (**)

Từ (*) và (**), suy ra \[\widehat {NFM} = \widehat {AIN}\].

Mà hai góc này ở vị trí đồng vị, do đó \[MF\,{\rm{//}}\,AC\].

c)

⦁ Gọi \(H\) là giao điểm của \(MN\) và \(OA.\)

Ta có \(AM = AN\) (tính chất hai tiếp tuyến cắt nhau) và \(OM = ON\) nên \(A,\,\,O\) cùng nằm trên đường trung trực của \(MN\) hay \(OA\) là đường trung trực của \(MN\).

Suy ra \[MN \bot OA\] hay \[HN \bot OA\].

Xét \[\Delta OHN\] và \[\Delta ONA\], có: \[\widehat {OHN} = \widehat {ONA} = 90^\circ \] và \[\widehat {AON}\] là góc chung

Do đó (g.g)

Suy ra \[\frac{{OH}}{{ON}} = \frac{{ON}}{{OA}}\] suy ra \[OH.OA = O{N^2} = {R^2}\] (3).

⦁ Ta có \(OC = OB,\,\,IC = IB\) (do \(I\) là trung điểm của \(BC),\) \(KC = KB\) (tính chất hai tiếp tuyến cắt nhau) nên ba điểm \(O,\,\,I,\,\,K\) thẳng hàng.

Xét \[\Delta OIB\] và \[\Delta OBK\], có: \[\widehat {OIB} = \widehat {OBK} = 90^\circ \] và \[\widehat {BOK}\] là góc chung

Do đó  (g.g)

Suy ra \[\frac{{OI}}{{OB}} = \frac{{OB}}{{OK}}\] suy ra \[OI.OK = O{B^2} = {R^2}\] (4).

Từ (3) và (4) suy ra \[OI.OK = OH.OA = {R^2}.\] Từ đó, ta có \[\frac{{OI}}{{OH}} = \frac{{OA}}{{OK}}\].

Xét \[\Delta OIA\] và \[\Delta OHK\] có: \[\widehat {AOK}\] là góc chung và \[\frac{{OI}}{{OH}} = \frac{{OA}}{{OK}}\]

Do đó  (c.g.c)

Suy ra \[\widehat {OHK} = \widehat {OIA} = 90^\circ \], suy ra \[HK \bot OA\].

Mà \[MN \bot OA\] tại \[H\] và \[MN\] cố định (do điểm \(A\) cố định), do đó \[K\] thuộc \[MN\] cố định.

Hướng dẫn giải

    a) Với \(a > 0,{\rm{ }}a \ne 1\), ta có:

\[A = \left( {\frac{{\sqrt a }}{2} - \frac{1}{{2\sqrt a }}} \right)\left( {\frac{{a - \sqrt a }}{{\sqrt a + 1}} - \frac{{a + \sqrt a }}{{\sqrt a - 1}}} \right)\]

   \[ = \left( {\frac{a}{{2\sqrt a }} - \frac{1}{{2\sqrt a }}} \right)\left[ {\frac{{\left( {\sqrt a - 1} \right)\sqrt a }}{{\sqrt a + 1}} - \frac{{\left( {\sqrt a + 1} \right)\sqrt a }}{{\sqrt a - 1}}} \right]\]

\[ = \frac{{a - 1}}{{2\sqrt a }}\left[ {\frac{{{{\left( {\sqrt a - 1} \right)}^2}\sqrt a }}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}} - \frac{{{{\left( {\sqrt a + 1} \right)}^2}\sqrt a }}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}} \right]\]

\[ = \frac{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}{{2\sqrt a }} \cdot \frac{{{{\left( {\sqrt a - 1} \right)}^2}\sqrt a - {{\left( {\sqrt a + 1} \right)}^2}\sqrt a }}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}\]

\[ = \frac{{{{\left( {\sqrt a - 1} \right)}^2}\sqrt a - {{\left( {\sqrt a + 1} \right)}^2}\sqrt a }}{{2\sqrt a }}\]

 \[ = \frac{{\left( {a - 2\sqrt a + 1} \right)\sqrt a - \left( {a + 2\sqrt a + 1} \right)\sqrt a }}{{2\sqrt a }}\]

\[ = \frac{{a\sqrt a - 2a + \sqrt a - a\sqrt a - 2a - \sqrt a }}{{2\sqrt a }}\]

\[ = \frac{{ - 4a}}{{2\sqrt a }}\]

\[ = - 2\sqrt a \].

Vậy \[A = - 2\sqrt a \] với \(a > 0,{\rm{ }}a \ne 1\).

b) Ta có: \(\left| {a - 1} \right| = 1\) suy ra \(a - 1 = 1\) hoặc \(a - 1 = - 1\).

Suy ra \(a = 2\) (thỏa mãn) hoặc \(a = 0\) (loại).

Thay \(a = 2\) vào \[A = - 2\sqrt a \] được \[A = - 2\sqrt 2 \].